

Bessel’s Function
Just imagine a dew drop falling from a leaf on the surface of an absolutely calm lake, creating short ripples in water which then fight among themselves and disappear in time. Such an amazing thing to watch but, today we will unfold the mathematics behind it.
The function which defines the phenomenon stated above or any acoustic activity on a circular membrane (exploited by most of the musical instruments) is called the Bessel’s function in the honour of the German astronomer Friedrich Wilhelm Bessel.
The Bessel function was first defined by famous mathematician Daniel Bernoulli and then generalized by Friedrich Bessel during an investigation of solutions of one of Kepler’s equations of planetary motion.
Bessel functions are used to solve in 3-D the wave equation at a given (harmonic) frequency. The solution is generally a sum of spherical Bessel’s functions that gives the acoustic pressure at a given location of the 3-D space.
The Bessel’s function is nothing but the canonical solutions of the Bessel’s differential equation-


for an arbitrary complex number α. Although α and −α produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of α. The most important cases are when α is an integer or half-integer.
The Bessel’s function can be categorized as follows-
| TYPE | FIRST KIND | SECOND KIND |
|---|---|---|
| Bessel functions | Jα | Yα |
| Modified Bessel functions | Iα | Kα |
| Hankel functions | H(1)α = Jα + iYα | H(2)α = Jα − iYα |
| Spherical Bessel functions | jn | yn |
| Spherical Hankel functions | h(1)n = jn + iyn | h(2)n = jn − iyn |
Bessel functions of the first kind of order n and -n –
We define the Bessel functions of the first kind as-
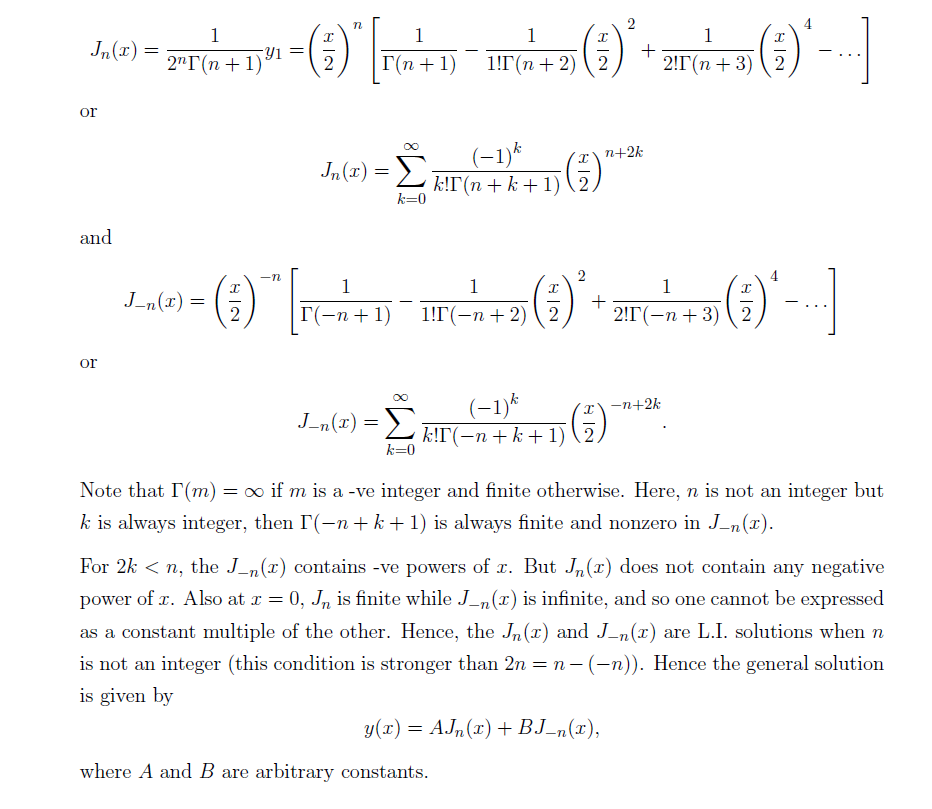

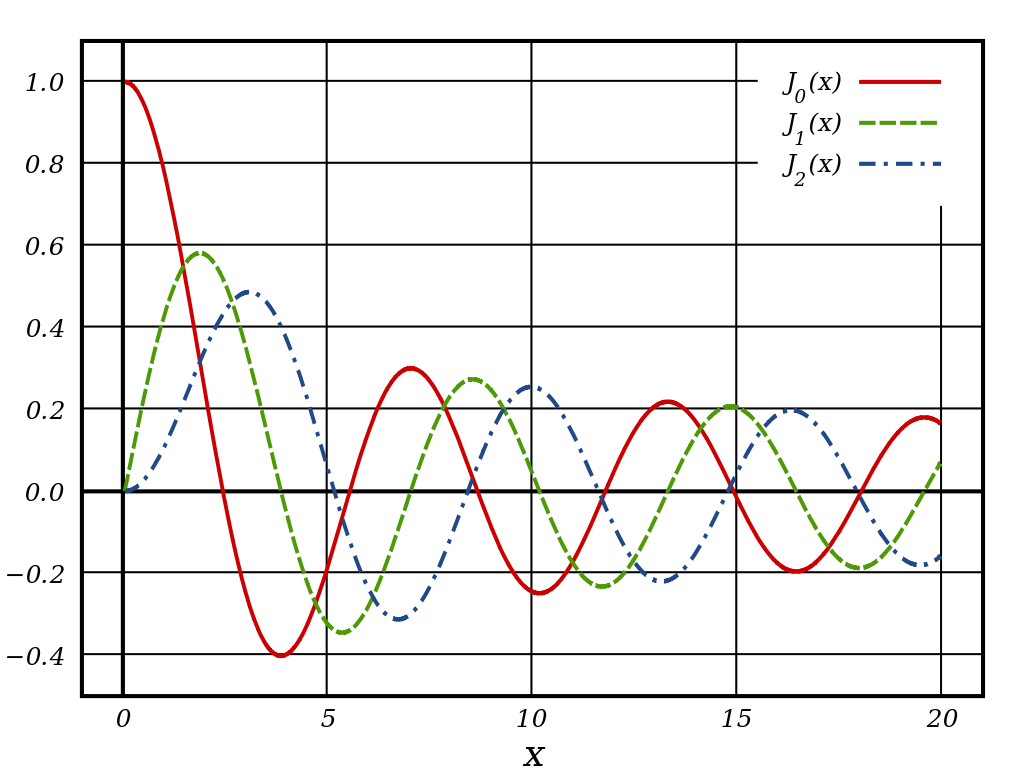

Bessel’s Function has a wide range of application in electromagnetic wave theory, solution to the radial Schrödinger equation (in spherical and cylindrical coordinates) for a free particle and many more. We will try understand few of them in the days to come.





One Comment
Srijita Paul
Presentation is excellent