FERMAT’S SPIRAL MANDALAS
Fermat’s spiral is similar to the Archimedean spiral. But an Archimedean spiral has always the same distance between neighboring arcs, which is not true for Fermat’s spiral. Like other spirals Fermat’s spiral is used for curvature continuous blending of curves.
A Fermat’s spiral or parabolic spiral is a plane curve named after Pierre de Fermat. Its polar coordinate representation is given by


A mandala is a geometric configuration of symbols. In various spiritual traditions, mandalas may be employed for focusing attention of practitioners and adepts, as a spiritual guidance tool, for establishing a sacred space and as an aid to meditation and trance induction.
Now lets explore Fermat’s Spiral as a method to create circular point figures and finally, a procedure of combining a series of spirals is proposed to form a mandala.
A Geometric Mandala
Point patterns are an interesting method to represent a variety of mathematical figures. Since they are capable of displaying properties of surface, direction, and line without being any of those, literally, the viewer connects the dots. One such example is Crova’s Disk.

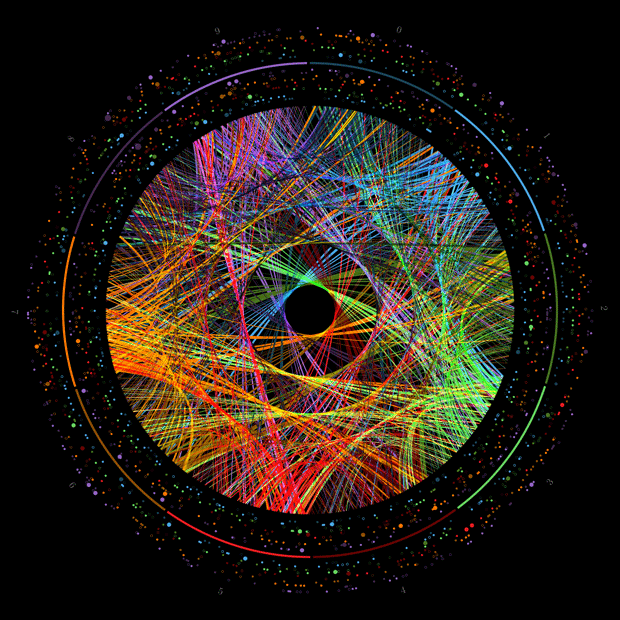
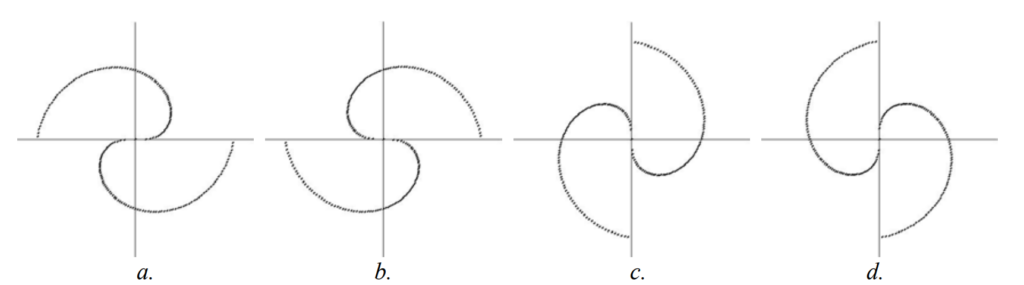
Since Fermat’s Spiral exhibited this interesting property of the placement of seeds and generating a variety of spiral and line patterns, a compositional procedure was investigated to repeat the spiral within a circular form, a geometric mandala. Figure 1a. displays the original spiral with at 0 and 180 degrees with a counterclockwise angle interval; Figure 1b. at 0 and 180 degrees clockwise; Figures 1c. and 1d. are the
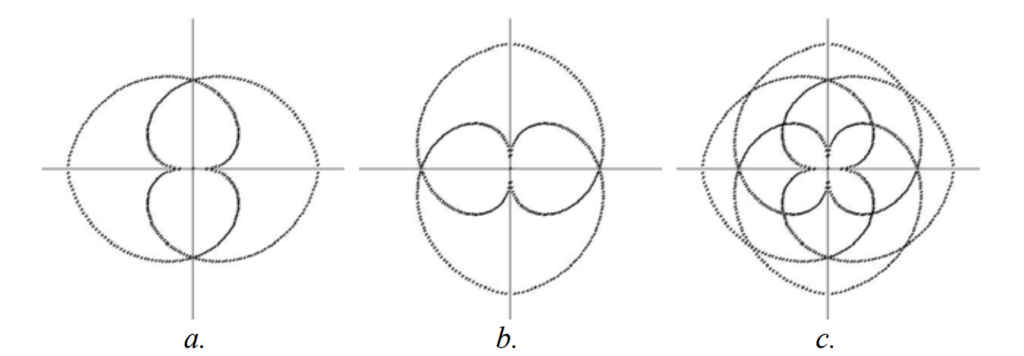
same as 1a. and 1b. but rotated 90 degrees counterclockwise. Figure 2a. displays the first four spirals combined; 2b. the last four spirals, and finally, 2c. all the spirals.


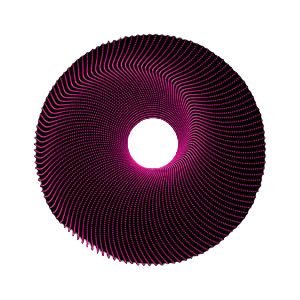
The relationship to mandalas is based on the circular form these figures take on, using the simple geometric definition of “mandala”; from the Sanskrit for circle. A mandala is a complex circular design, intended to draw the eye inward to its center having symmetrical and radial balance. The Fermat’s Spiral in particular is a natural basis for this inward draw.


This figure displays a series of mandalas based on some of the spirals suggested by Dixon. They include √2, 254.6 degrees; e, 132.5 degrees; plus variations: e/2, 264.9 degrees, and e/4, 169.8 degrees. As the original spirals demonstrated interesting patterns of inner spirals and lines, the combined version also beginning to exhibit patterns that included: rays, pedals, zig-zags, squiggles, hexagons, swirls, and spirals in all directions and length. The generation and initial inspection of some 900 mandalas shown a large number of such combinations of elements; some congregating around the center, some along the edges, and some in between. Also noted was that a minor change of only 0.1 degree would generate a much different pattern. Currently, no attempt has been made to understand the mathematical relationship between the angle of divergence and the patterns generated.


Division of the plane
A complete Fermat’s spiral (both branches) is a smooth double point free curve, in contrast with the Archimedean and hyperbolic spiral. It divides the plane (like a line or circle or parabola) into two connected regions. But this division is less obvious than the division by a line or circle or parabola. It is not obvious to which side a chosen point belongs.
- at the origin an inflection point and the x-axis is its tangent there.
KUDOS TO: Robert J. Krawczyk
College of Architecture, Illinois Institute of Technology