

The Navier-Stokes Equations
Fluid Dynamics and the Navier-Stokes Equations
The Navier-Stokes equations, developed by Claude-Louis Navier and George Gabriel Stokes in 1822, are equations which can be used to determine the velocity vector field that applies to a fluid, given some initial conditions. They arise from the application of Newton’s second law in combination with a fluid stress (due to viscosity) and a pressure term. For almost all real situations, they result in a system of nonlinear partial differential equations; however, with certain simplifications (such as 1-dimensional motion) they can sometimes be reduced to linear differential equations. Usually, however, they remain nonlinear, which makes them difficult or impossible to solve; this is what causes the turbulence and unpredictability in their results.
Derivation of the Navier-Stokes Equations
The Navier-Stokes equations can be derived from the basic conservation and continuity equations applied to properties of fluids. In order to derive the equations of fluid motion, we must first derive the continuity equation (which dictates conditions under which things are conserved), apply the equation to conservation of mass and momentum, and finally combine the conservation equations with a physical understanding of what a fluid is.
Continuity Equation
The basic continuity equation is an equation which describes the change of an intensive property L. An intensive property is something which is independent of the amount of material you have. For instance, temperature would be an intensive property; heat would be the corresponding extensive property. The volume Ω is assumed to be of any form; its bounding surface area is referred to as ∂Ω. The continuity equation derived can later be applied to mass and momentum.
General Form of the Navier-Stokes Equation
The stress tensor σ denoted above is often divided into two terms of interest in the general form of the Navier-Stokes equation. The two terms are the volumetric stress tensor, which tends to change the volume of the body, and the stress deviator tensor, which tends to deform the body. The volumetric stress tensor represents the force which sets the volume of the body (namely, the pressure forces). The stress deviator tensor represents the forces which determine body deformation and movement, and is composed of the shear stresses on the fluid. Thus, σ is broken down into
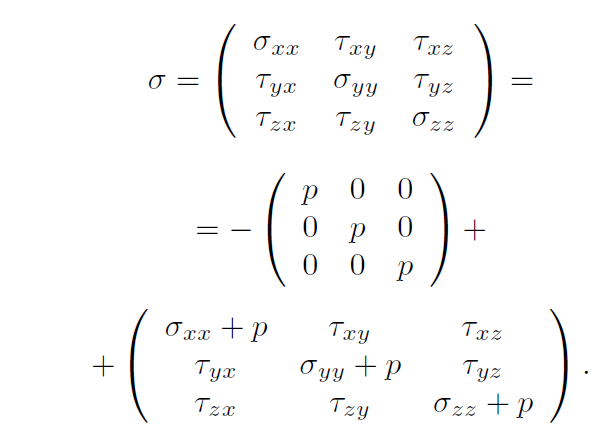

Denoting the stress deviator tensor as T, we can make the substitution
σ = −pI + T.
Substituting this into the previous equation, we arrive at the most general form of the Navier-Stokes equation:
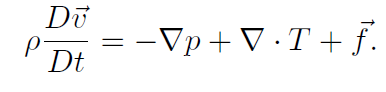

Although this is the general form of the Navier-Stokes equation, it cannot be applied until it has been more specified. First off, depending on the type of fluid, an expression must be determined for the stress tensor T; secondly, if the fluid is not assumed to be incompressible, an equation of state and an equation dictating conservation of energy are necessary.

Physical Explanation of the Navier-Stokes Equation
The Navier-Stokes equation makes a surprising amount of intuitive sense given the complexity of what it is modeling. The left hand side of the equation,
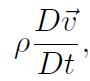

is the force on each fluid particle. The equation states that the force is composed of three terms:
• −∇p: A pressure term (also known as the volumetric stress tensor) which prevents motion due to normal stresses. The fluid presses against itself and keeps it from shrinking in volume.
• ∇ · T: A stress term (known as the stress deviator tensor) which causes motion due to horizontal friction and shear stresses. The shear stress causes turbulence and viscous flows – if you drag your hand through a liquid, you will note that the moving liquid also causes nearby liquid to start moving in the same direction. Turbulence is the result of the shear stress.
•~f: The force term which is acting on every single fluid particle. This intuitively explains turbulent flows and some common scenarios. For example, if water is sitting in a cup, the force (gravity) ρg is equal to the pressure term because d/dz (ρgz) = ρg. Thus, since gravity is equivalent to the pressure, the fluid will sit still, which is indeed what we observe when water is sitting in a cup.


Due to the complex nature of the Navier-Stokes equations, analytical solutions range from difficult to practically impossible, so the most common way to make use of the Navier-Stokes equations is through simulation and approximation. A number of simulation methods exist, and in the next section, we will examine one of the algorithms often used in computer graphics and interactive applications.


Waves follow our boat as we meander across the lake, and turbulent air currents follow our flight in a modern jet. Mathematicians and physicists believe that an explanation for and the prediction of both the breeze and the turbulence can be found through an understanding of solutions to the Navier-Stokes equations. Although these equations were written down in the 19th Century, our understanding of them remains minimal.
The challenge is to make substantial progress toward a mathematical theory which will unlock the secrets hidden in the Navier-Stokes equations.







5 Comments
Ankita paul
Really productive…
gate.io
Your article helped me a lot. what do you think? I want to share your article to my website: gate.io
ar criptomoedas
Reading your article helped me a lot and I agree with you. But I still have some doubts, can you clarify for me? I’ll keep an eye out for your answers.
gat io
Reading your article helped me a lot and I agree with you. But I still have some doubts, can you clarify for me? I’ll keep an eye out for your answers.
rbis listing
Reading your article helped me a lot and I agree with you. But I still have some doubts, can you clarify for me? I’ll keep an eye out for your answers.