In additive number theory we make reference to facts about addition in contradistinction to multiplicative number theory, the foundations of which were laid by Euclid at about 300 B.C. Whereas one of the principal concerns of the latter theory is the decomposition of numbers into prime factors, additive number theory deals with the decomposition of numbers into summands. It asks such questions as: in how many ways can a given natural number be expressed as the sum of other natural numbers? Of course the decomposition into primary summands is trivial; it is therefore of interest to restrict in some way the nature of the summands (such as odd numbers or even numbers or perfect squares) or the number of summands allowed. These are questions typical of those which will arise in this course. We shall have occasion to study the properties of V-functions and their numerous applications to number theory, in particular the theory of quadratic residues.

The Dirichlet product of arithmetic functions
The two obvious operations on the set of arithmetic functions are pointwise addition and multiplication. The constant functions f = 0 and f = 1 are neutral elements with respect to these operations, and the additive and multiplicative inverses of a function f are given by −f and 1/f, respectively. While these operations are sometimes useful, by far the most important operation among arithmetic functions is the so-called Dirichlet product, an operation that, at first glance, appears mysterious and unmotivated, but which has proved to be an extremely useful tool in the theory of arithmetic functions.
Definition. Given two arithmetic functions f and g, the Dirichlet product (or Dirichlet convolution) of f and g, denoted by f ∗ g, is the arithmetic function defined by


One motivation for introducing this product is the fact that the definitions of many common arithmetic functions have the form of a Dirichlet product, and that many identities among arithmetic functions can be written concisely as identities involving Dirichlet products.
The Dirichlet inverse of λ. Since µ ∗ 1 = e, the function 1 is the Dirichlet inverse of the Moebius function. To find the Dirichlet inverse of λ, i.e., the unique function f such that λ ∗ f = e, note first that since λ and e are both multiplicative, f must be multiplicative as well, and it therefore suffices to evaluate f at prime powers. Now, for any prime power pm,
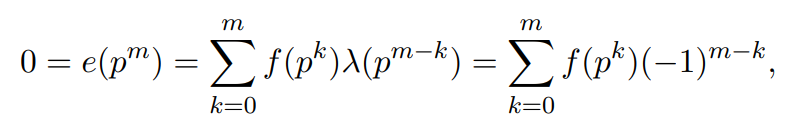

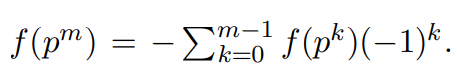

This implies f(p) = 1, and by induction f(pm) = 0 for m ≥ 2. Hence f is the characteristic function of the square free numbers, i.e., λ−1 = µ2.
Evaluating Dirichlet products of multiplicative functions. Since the Dirichlet product of multiplicative functions is multiplicative, and since a multiplicative function is determined by its values on prime powers, to evaluate a product f ∗ g with both f and g multiplicative, it suffices to compute the values of f ∗ g at prime powers. By comparing these values to those of familiar arithmetic functions, one can often identify f ∗ g in terms of familiar arithmetic functions.
Dirichlet Series

Given an arithmetic function f(n), the series
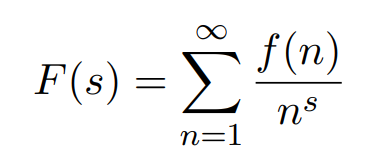

is called the Dirichlet series associated with f. A Dirichlet series can be regarded as a purely formal infinite series (i.e., ignoring questions about convergence), or as a function of the complex variable s, defined in the region in which the series converges. The variable s is usually written as
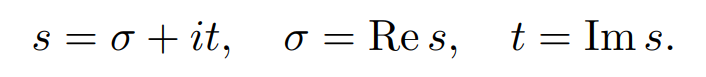

Dirichlet series serve as a type of generating functions for arithmetic functions, adapted to the multiplicative structure of the integers, and they play a role similar to that of ordinary generating functions in combinatorics. For example, just as ordinary generating functions can be used to prove combinatorial identities, Dirichlet series can be applied to discover and prove identities among arithmetic functions.
On a more sophisticated level, the analytic properties of a Dirichlet series, regarded as a function of the complex variable s, can be exploited to obtain information on the behavior of partial sums


of arithmetic functions. This is how Hadamard and de la Vall’ee Poussin obtained the first proof of the Prime Number Theorem. In fact, most analytic proofs of the Prime Number Theorem (including the one we shall give in the following chapter) proceed by relating the partial sums


to a complex integral involving the Dirichlet series
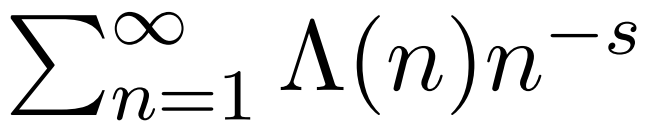

and evaluating that integral by analytic techniques. The most famous Dirichlet series is the Riemann zeta function ζ(s), defined as the Dirichlet series associated with the constant function,


where σ is the real part of s.
