Newton’s Three Body Problem

The classical three-body problem arose in an attempt to understand the effect of the Sun on the Moon’s Keplerian orbit around the Earth. It has attracted the attention of some of the best physicists and mathematicians and led to the discovery of ‘chaos’. We survey the three-body problem in its historical context and use it to introduce several ideas and techniques that have been developed to understand classical mechanical systems.

The study of the three-body problem led to the discovery of the planet Neptune, it explains the location and stability of the Trojan asteroids and has furthered our understanding of the stability of the solar system. Quantum mechanical variants of the three-body problem are relevant to the helium atom and water molecule.

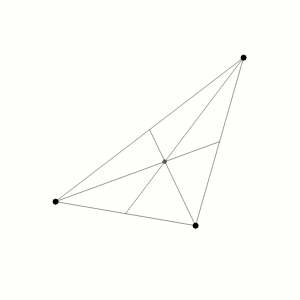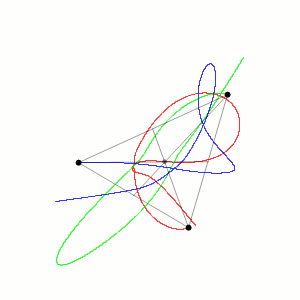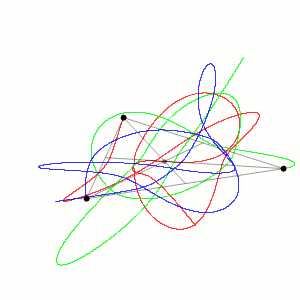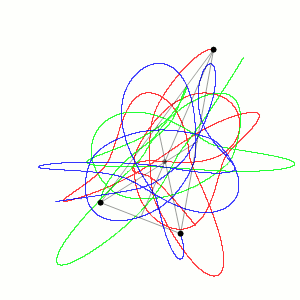
We consider the problem of three point masses (ma with position vectors ra for a = 1, 2, 3) moving under their mutual gravitational attraction. This system has 9 degrees of freedom, whose dynamics is determined by 9 coupled second order nonlinear ODEs:

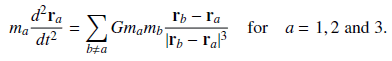
As before, the three components of momentum,

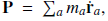
three components of angular momentum,

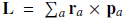
and energy,

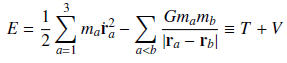
Wolfgang Pauli (1926) derived the quantum mechanical spectrum of the Hydrogen atom using the relation between E, L2 and A2 before the development of the Schrodinger equation. Indeed, if we postulate circular Bohr orbits which have zero eccentricity (A = 0) and quantized angular momentum L^2 = n^2(h/2pi)^2, then En = − (mα^2)/ (2(h/2pi)^2n^2) where α = e^2/4πϵ0 is the electromagnetic analogue of Gm1m2.

General solutions

There is no general analytical solution to the three-body problem given by simple algebraic expressions and integrals. Moreover, the motion of three bodies is generally non-repeating, except in special cases.

On the other hand, in 1912 the Finnish mathematician Karl Fritiof Sundman proved that there exists a series solution in powers of t^1/3 for the 3-body problem. This series converges for all real t, except for initial conditions corresponding to zero angular momentum. (In practice the latter restriction is insignificant since such initial conditions are rare, having Lebesgue measure zero.)

An important issue in proving this result is the fact that the radius of convergence for this series is determined by the distance to the nearest singularity. Therefore, it is necessary to study the possible singularities of the 3-body problems. As it will be briefly discussed below, the only singularities in the 3-body problem are binary collisions (collisions between two particles at an instant) and triple collisions (collisions between three particles at an instant).

Collisions, whether binary or triple (in fact, any number), are somewhat improbable, since it has been shown that they correspond to a set of initial conditions of measure zero. However, there is no criterion known to be put on the initial state in order to avoid collisions for the corresponding solution. So Sundman’s strategy consisted of the following steps:

1. Using an appropriate change of variables to continue analyzing the solution beyond the binary collision, in a process known as regularization.
2. Proving that triple collisions only occur when the angular momentum L vanishes. By restricting the initial data to L ≠ 0, he removed all real singularities from the transformed equations for the 3-body problem.
3. Showing that if L ≠ 0, then not only can there be no triple collision, but the system is strictly bounded away from a triple collision. This implies, by using Cauchy’s existence theorem for differential equations, that there are no complex singularities in a strip (depending on the value of L) in the complex plane centered around the real axis (shades of Kovalevskaya).
4. Find a conformal transformation that maps this strip into the unit disc. For example, if s = t^1/3 (the new variable after the regularization) and if |ln s| ≤ β, then this map is given by

Unfortunately, the corresponding series converges very slowly. That is, obtaining a value of meaningful precision requires so many terms that this solution is of little practical use. Indeed, in 1930, David Beloriszky calculated that if Sundman’s series were to be used for astronomical observations, then the computations would involve at least 10^8000000 terms.

n-body problem

The three-body problem is a special case of the n-body problem, which describes how n objects will move under one of the physical forces, such as gravity. These problems have a global analytical solution in the form of a convergent power series, as was proven by Karl F. Sundman for n = 3 and by Qiudong Wang for n > 3. However, the Sundman and Wang series converge so slowly that they are useless for practical purposes; therefore, it is currently necessary to approximate solutions by numerical analysis in the form of numerical integration or, for some cases, classical trigonometric series approximations. Atomic systems, e.g. atoms, ions, and molecules, can be treated in terms of the quantum n-body problem. Among classical physical systems, the n-body problem usually refers to a galaxy or to a cluster of galaxies; planetary systems, such as stars, planets, and their satellites, can also be treated as n-body systems. Some applications are conveniently treated by perturbation theory, in which the system is considered as a two-body problem plus additional forces causing deviations from a hypothetical unperturbed two-body trajectory.