

The Knight’s Tour
The knight’s tour problem is the mathematical problem of finding a knight’s tour, and probably making knight the most interesting piece on the chess board. The knight visits every square exactly once, if the knight ends on a square that is one knight’s move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed; otherwise, it is open.
The knight’s tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight’s tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight’s tour problem can be solved in linear time.
Hamiltonian Path Problem
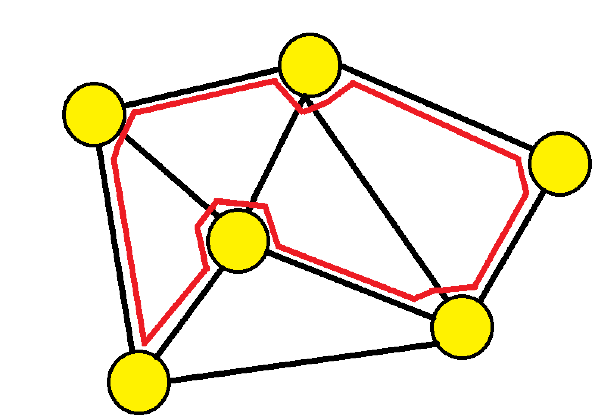

In Graph Theory, a graph is usually defined to be a collection of nodes or vertices and the set of edges which define which nodes are connected with each other. So we use a well known notation of representing a graph G = (V,E) where V = { v1, v2, v3, … , vn } and E = {(i, j)|i ∈ V and j ∈ V and i and j is connected}.
Hamiltonian Path is defined to be a single path that visits every node in the given graph, or a permutation of nodes in such a way that for every adjacent node in the permutation there is an edge defined in the graph. Notice that it does not make much sense in repeating the same paths. In order to avoid this repetition, we permute with |V|C2 combinations of starting and ending vertices.
Simple way of solving the Hamiltonian Path problem would be to permutate all possible paths and see if edges exist on all the adjacent nodes in the permutation. If the graph is a complete graph, then naturally all generated permutations would quality as a Hamiltonian path.
For example. let us find a Hamiltonian path in graph G = (V,E) where V = {1,2,3,4} and E = {(1,2),(2,3),(3,4)}. Just by inspection, we can easily see that the Hamiltonian path exists in permutation 1234. The given algorithm will first generate the following permutations based on the combinations:
1342 1432 1243 1423 1234 1324 2143 2413 2134 2314 3124 3214
The number that has to be generated is (|V|C2 ) (|V| – 2)!
Existence


Schwenk proved that for any m × n board with m ≤ n, a closed knight’s tour is always possible unless one or more of these three conditions are met:
- m and n are both odd
- m = 1, 2, or 4
- m = 3 and n = 4, 6, or 8.
Cull and Conrad proved that on any rectangular board whose smaller dimension is at least 5, there is a (possibly open) knight’s tour.
| n | Number of directed tours (open and closed) on an n × n board (sequence A165134 in the OEIS) |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 1,728 |
| 6 | 6,637,920 |
| 7 | 165,575,218,320 |
| 8 | 19,591,828,170,979,904 |
Neural network solutions
The neural network is designed such that each legal knight’s move on the chessboard is represented by a neuron. Therefore, the network basically takes the shape of the knight’s graph over an n×n chess board. (A knight’s graph is simply the set of all knight moves on the board)
Each neuron can be either “active” or “inactive” (output of 1 or 0). If a neuron is active, it is considered part of the solution to the knight’s tour. Once the network is started, each active neuron is configured so that it reaches a “stable” state if and only if it has exactly two neighboring neurons that are also active (otherwise, the state of the neuron changes). When the entire network is stable, a solution is obtained. The complete transition rules are as follows:
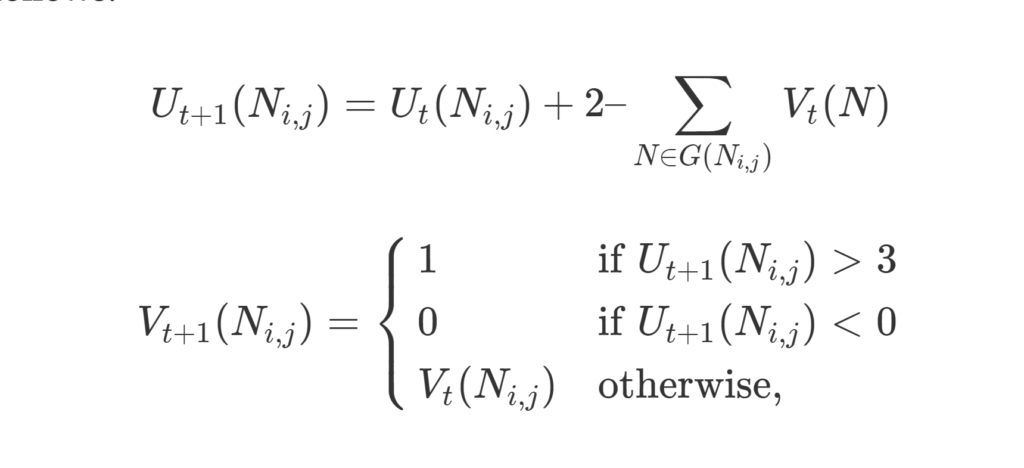

where t represents time (incrementing in discrete intervals), U(Ni,j) is the state of the neuron connecting square i to square j, V(Ni,j) is the output of the neuron from i to j, and G(Ni,j) is the set of “neighbors” of the neuron (all neurons that share a vertex with Ni,j).
Code For Knight’s Tour
// Java program for Knight Tour problem
class KnightTour {
static int N = 8;
/* A utility function to check if i,j are
valid indexes for N*N chessboard */
static boolean isSafe(int x, int y, int sol[][])
{
return (x >= 0 && x < N && y >= 0 && y < N
&& sol[x][y] == -1);
}
/* A utility function to print solution
matrix sol[N][N] */
static void printSolution(int sol[][])
{
for (int x = 0; x < N; x++) {
for (int y = 0; y < N; y++)
System.out.print(sol[x][y] + " ");
System.out.println();
}
}
/* This function solves the Knight Tour problem
using Backtracking. This function mainly
uses solveKTUtil() to solve the problem. It
returns false if no complete tour is possible,
otherwise return true and prints the tour.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions. */
static boolean solveKT()
{
int sol[][] = new int[8][8];
/* Initialization of solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x][y] = -1;
/* xMove[] and yMove[] define next move of Knight.
xMove[] is for next value of x coordinate
yMove[] is for next value of y coordinate */
int xMove[] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int yMove[] = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Since the Knight is initially at the first block
sol[0][0] = 0;
/* Start from 0,0 and explore all tours using
solveKTUtil() */
if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) {
System.out.println("Solution does not exist");
return false;
}
else
printSolution(sol);
return true;
}
/* A recursive utility function to solve Knight
Tour problem */
static boolean solveKTUtil(int x, int y, int movei,
int sol[][], int xMove[],
int yMove[])
{
int k, next_x, next_y;
if (movei == N * N)
return true;
/* Try all next moves from the current coordinate
x, y */
for (k = 0; k < 8; k++) {
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol)) {
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1,
sol, xMove, yMove))
return true;
else
sol[next_x][next_y]
= -1; // backtracking
}
}
return false;
}
/* Driver Code */
public static void main(String args[])
{
// Function Call
solveKT();
}
}









