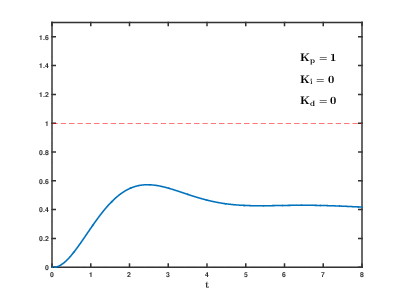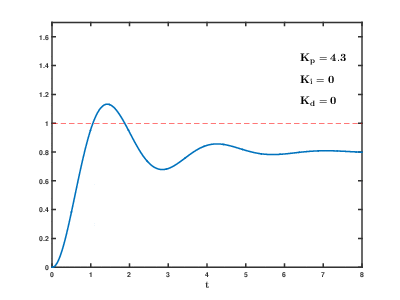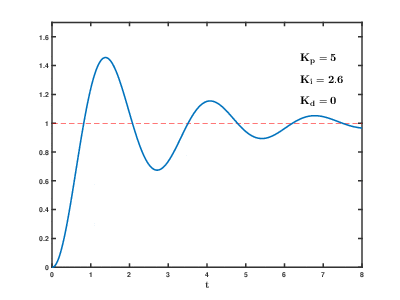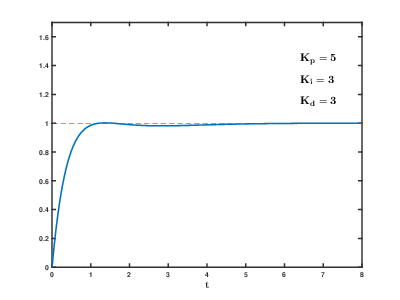
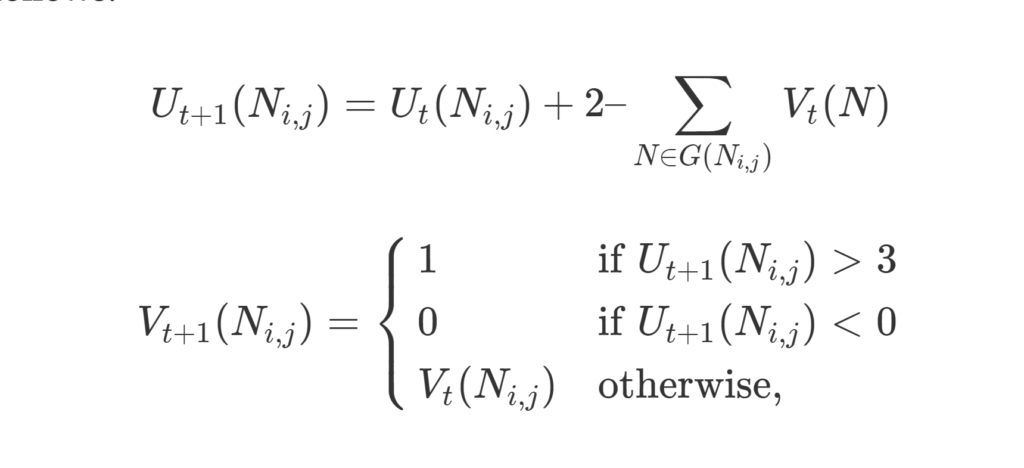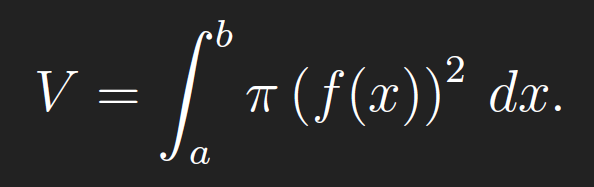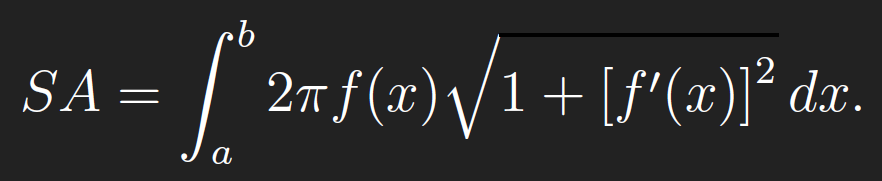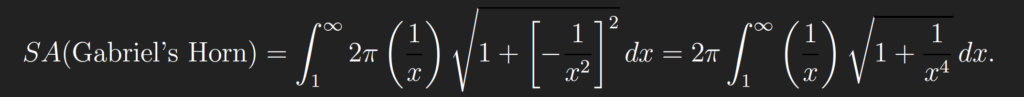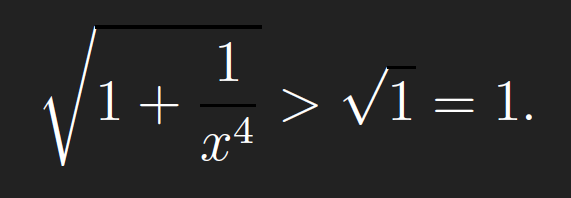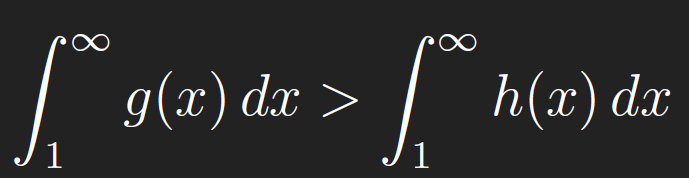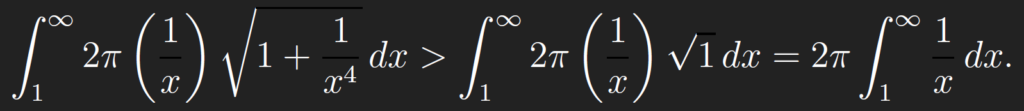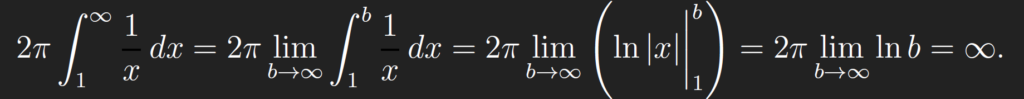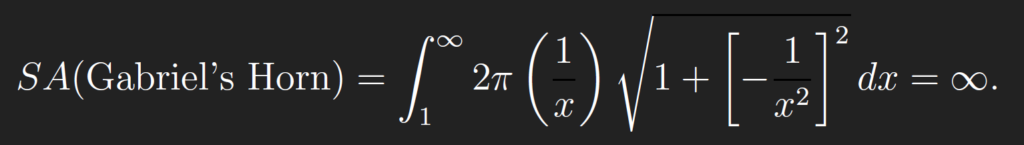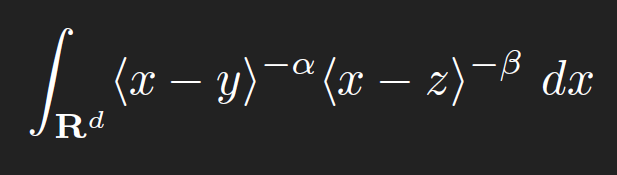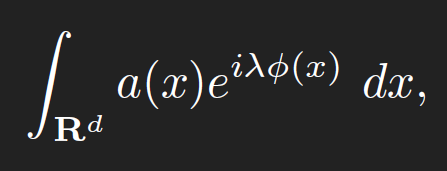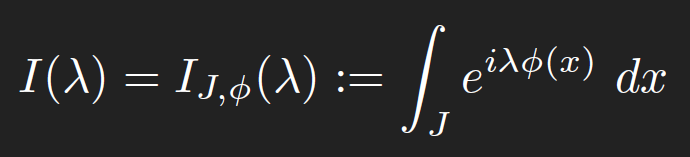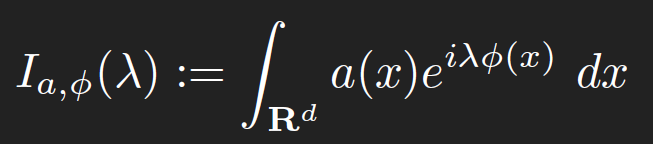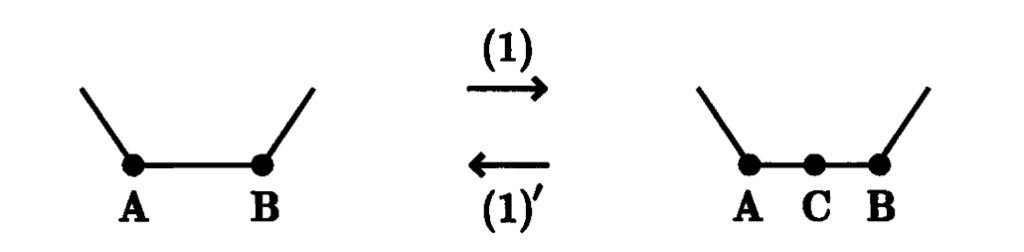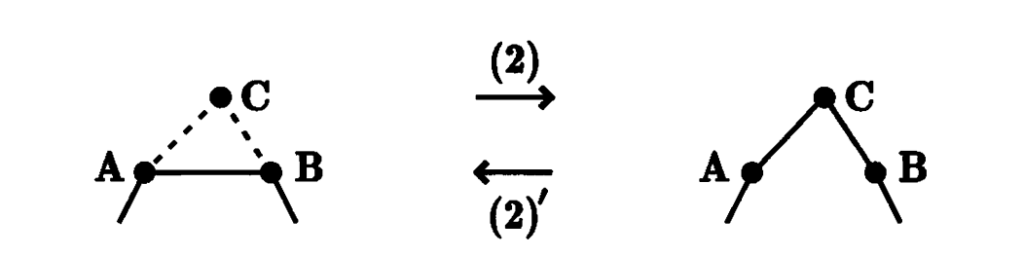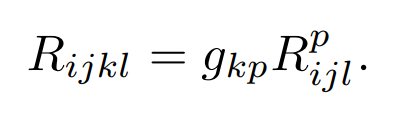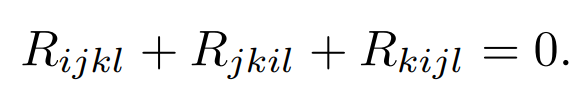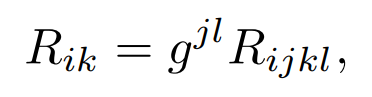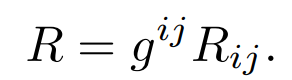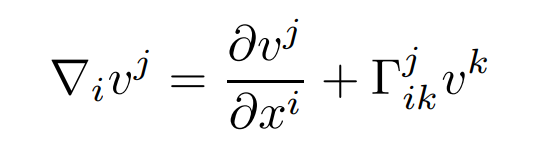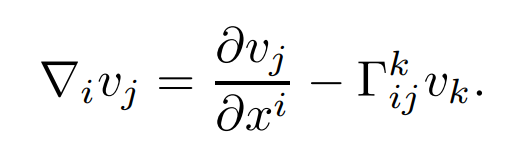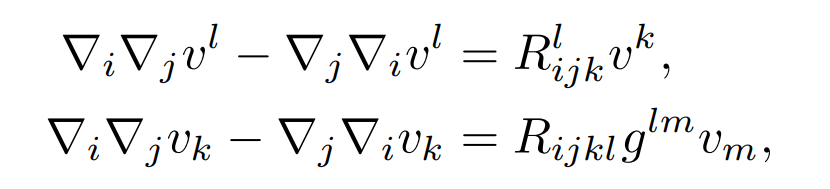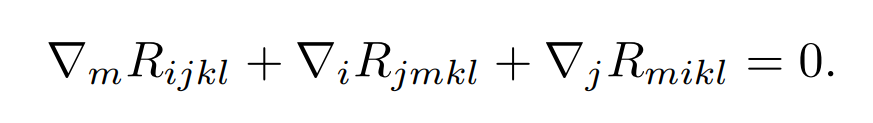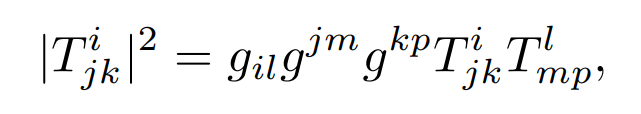Birch and Swinnerton-Dyer Conjecture
This conjecture connects the rank of the group of rational points to the number of points on an elliptic curve mod p and is backed up by a wealth of experimental evidence. Elliptic curves are essential mathematical objects that appear in numerous contexts, including Wiles’ demonstration of the Fermat Conjecture, the factorization of numbers into primes, and cryptography, to name just three. Elliptic curves are described by cubic equations in two variables.


Bryan John Birch
Professor Sir Peter Swinnerton-Dyer


Early History
Problems on curves of genus 1 feature prominently in Diophantus’ Arithmetica. It is easy to see that a straight line meets an elliptic curve in three points (counting multiplicity) so that if two of the points are rational then so is the third. In particular, if a tangent is taken at a rational point, then it meets the curve again in a rational point. Diophantus implicitly used this method to obtain a second solution from a first. He did not iterate this process, however, and it was Fermat who first realized that one can sometimes obtain infinitely many solutions in this way. Fermat also introduced a method of ‘descent’ that sometimes permits one to show that the number of solutions is finite or even zero.
One very old problem concerned with rational points on elliptic curves is the congruent number problem. One way of stating it is to ask which rational integers can occur as the areas of right angled triangles with rational length sides. Such integers are called congruent numbers.
Recent History
It was the 1901 paper of Poincare that started the modern theory of rational points on curves and that first raised questions about the minimal number of generators of C(Q). The conjecture itself was first stated in the form we have given
in the early 1960s. It was found experimentally using one of the early EDSAC computers at Cambridge. The first general result proved was for elliptic curves with complex multiplication. The curves with complex multiplication fall into a finite number of families including {y2 = x3 − Dx} and {y 2 = x3 − k} for varying D, k ≠ 0. This theorem was proved in 1976 and is due to Coates and Wiles. It states that if C is a curve with complex multiplication and L(C, 1) ≠ 0, then C(Q) is finite. In 1983 Gross and Zagier showed that if C is a modular elliptic curve and L(C, 1) = 0 but L0 (C, 1) ≠ 0, then an earlier construction of Heegner actually gives a rational point of infinite order. Using new ideas together with this result, Kolyvagin showed in 1990 that for modular elliptic curves, if L(C, 1) ≠ 0Rational Points on Higher-Dimensional Varieties
We began by discussing the diophantine properties of curves, and we have seen that the problem of giving a criterion for whether C(Q) is finite or not is only an issue for curves of genus 1. Moreover, according to the conjecture above, in the case of genus 1, C(Q) is finite if and only if L(C, 1) ≠ 0. In higher dimensions, if V is an algebraic variety, it is conjectured that if we remove from V (the closure of) all subvarieties that are images of P1 or of abelian varieties, then the remaining open variety W should have the property that W(Q) is finite. This has been proved by Faltings in the case where V is itself a subvariety of an abelian variety.
This suggests that to find infinitely many points on V one should look for rational curves or abelian varieties in V . In the latter case we can hope to use methods related to the Birch and Swinnerton-Dyer conjecture to find rational points on the abelian variety. As an example of this, consider the conjecture of Euler from 1769 that x4 +y4 +z4 = t4 has no non-trivial solutions. By finding a curve of genus 1 on
the surface and a point of infinite order on this curve, Elkies found the solution 26824404 + 153656394 + 187967604 = 206156734.
His argument shows that there are infinitely many solutions to Euler’s equation. In conclusion, although there has been some success in the last fifty years in limiting the number of rational points on varieties, there are still almost no methods for finding such points. It is to be hoped that a proof of the Birch and Swinnerton Dyer conjecture will give some insight concerning this general problem.Conjecture (Birch and Swinnerton-Dyer)
The Taylor expansion of L(C, s) at s = 1 has the form L(C, s) = c(s − 1)r + higher order terms with c ≠ 0 and r = rank(C(Q)).
This problem is still unsolved and is one the seven millennial problems of the Clay Mathematical Institute.
The Knight’s Tour
The knight’s tour problem is the mathematical problem of finding a knight’s tour, and probably making knight the most interesting piece on the chess board. The knight visits every square exactly once, if the knight ends on a square that is one knight’s move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed; otherwise, it is open.
The knight’s tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight’s tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight’s tour problem can be solved in linear time.
Hamiltonian Path Problem


In Graph Theory, a graph is usually defined to be a collection of nodes or vertices and the set of edges which define which nodes are connected with each other. So we use a well known notation of representing a graph G = (V,E) where V = { v1, v2, v3, … , vn } and E = {(i, j)|i ∈ V and j ∈ V and i and j is connected}.
Hamiltonian Path is defined to be a single path that visits every node in the given graph, or a permutation of nodes in such a way that for every adjacent node in the permutation there is an edge defined in the graph. Notice that it does not make much sense in repeating the same paths. In order to avoid this repetition, we permute with |V|C2 combinations of starting and ending vertices.
Simple way of solving the Hamiltonian Path problem would be to permutate all possible paths and see if edges exist on all the adjacent nodes in the permutation. If the graph is a complete graph, then naturally all generated permutations would quality as a Hamiltonian path.
For example. let us find a Hamiltonian path in graph G = (V,E) where V = {1,2,3,4} and E = {(1,2),(2,3),(3,4)}. Just by inspection, we can easily see that the Hamiltonian path exists in permutation 1234. The given algorithm will first generate the following permutations based on the combinations:
1342 1432 1243 1423 1234 1324 2143 2413 2134 2314 3124 3214The number that has to be generated is (|V|C2 ) (|V| – 2)!
Existence


Schwenk proved that for any m × n board with m ≤ n, a closed knight’s tour is always possible unless one or more of these three conditions are met:
- m and n are both odd
- m = 1, 2, or 4
- m = 3 and n = 4, 6, or 8.
Cull and Conrad proved that on any rectangular board whose smaller dimension is at least 5, there is a (possibly open) knight’s tour.
n Number of directed tours (open and closed)
on an n × n board
(sequence A165134 in the OEIS)1 1 2 0 3 0 4 0 5 1,728 6 6,637,920 7 165,575,218,320 8 19,591,828,170,979,904 Neural network solutions
The neural network is designed such that each legal knight’s move on the chessboard is represented by a neuron. Therefore, the network basically takes the shape of the knight’s graph over an n×n chess board. (A knight’s graph is simply the set of all knight moves on the board)
Each neuron can be either “active” or “inactive” (output of 1 or 0). If a neuron is active, it is considered part of the solution to the knight’s tour. Once the network is started, each active neuron is configured so that it reaches a “stable” state if and only if it has exactly two neighboring neurons that are also active (otherwise, the state of the neuron changes). When the entire network is stable, a solution is obtained. The complete transition rules are as follows:


where t represents time (incrementing in discrete intervals), U(Ni,j) is the state of the neuron connecting square i to square j, V(Ni,j) is the output of the neuron from i to j, and G(Ni,j) is the set of “neighbors” of the neuron (all neurons that share a vertex with Ni,j).
Code For Knight’s Tour
// Java program for Knight Tour problem class KnightTour { static int N = 8; /* A utility function to check if i,j are valid indexes for N*N chessboard */ static boolean isSafe(int x, int y, int sol[][]) { return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1); } /* A utility function to print solution matrix sol[N][N] */ static void printSolution(int sol[][]) { for (int x = 0; x < N; x++) { for (int y = 0; y < N; y++) System.out.print(sol[x][y] + " "); System.out.println(); } } /* This function solves the Knight Tour problem using Backtracking. This function mainly uses solveKTUtil() to solve the problem. It returns false if no complete tour is possible, otherwise return true and prints the tour. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ static boolean solveKT() { int sol[][] = new int[8][8]; /* Initialization of solution matrix */ for (int x = 0; x < N; x++) for (int y = 0; y < N; y++) sol[x][y] = -1; /* xMove[] and yMove[] define next move of Knight. xMove[] is for next value of x coordinate yMove[] is for next value of y coordinate */ int xMove[] = { 2, 1, -1, -2, -2, -1, 1, 2 }; int yMove[] = { 1, 2, 2, 1, -1, -2, -2, -1 }; // Since the Knight is initially at the first block sol[0][0] = 0; /* Start from 0,0 and explore all tours using solveKTUtil() */ if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) { System.out.println("Solution does not exist"); return false; } else printSolution(sol); return true; } /* A recursive utility function to solve Knight Tour problem */ static boolean solveKTUtil(int x, int y, int movei, int sol[][], int xMove[], int yMove[]) { int k, next_x, next_y; if (movei == N * N) return true; /* Try all next moves from the current coordinate x, y */ for (k = 0; k < 8; k++) { next_x = x + xMove[k]; next_y = y + yMove[k]; if (isSafe(next_x, next_y, sol)) { sol[next_x][next_y] = movei; if (solveKTUtil(next_x, next_y, movei + 1, sol, xMove, yMove)) return true; else sol[next_x][next_y] = -1; // backtracking } } return false; } /* Driver Code */ public static void main(String args[]) { // Function Call solveKT(); } }GABRIEL’S HORN
The Painter’s Paradox is based on the fact that Gabriel’s horn has infinite surface area and finite volume and the paradox emerges when finite contextual interpretations of area and volume are attributed to the intangible object of Gabriel’s horn. Mathematically, this paradox is a result of generalized area and volume concepts using integral calculus, as the Gabriel’s horn has a convergent series associated with volume and a divergent series associated with surface area. The dimensions of this object, which are in the heart of the above mentioned paradox, were first studied by Torricelli. To situate the paradox historically, we provide a brief overview of the development of the notion of infinity in mathematics and the debate around Torricelli’s discovery.
Gabriel and His Horn


Gabriel was an archangel, as the Bible tells us, who “used a horn to announce news that was sometimes heartening (e.g., the birth of Christ in Luke l) and sometimes fatalistic (e.g., Armageddon in Revelation 8-11)”.
Torricelli’s Long Horn
In 1641 Evangelista Torricelli showed that a certain solid of infinite length, now known as the Gabriel’s horn, which he called the acute hyperbolic solid, has a finite volume. In De solido hyperbolico acuto he defined an acute hyperbolic solid as the solid generated when a hyperbola is rotated around an asymptote and stated the following theorem:
THEOREM: An acute hyperbolic solid, infinitely long [infinite longum], cut by a plane [perpendicular] to the axis, together with a cylinder of the same base, is equal to that right cylinder of which the base is the latus transversum of the hyperbola (that is, the diameter of the hyperbola), and of which the altitude is equal to the radius of the base of this acute body.


The Queer Volume
Construct the surface of revolution given by rotating the function f(x) = 1/x on [1,∞) around the x-axis. The volume of a surface of revolution given by rotating the function f(x), de fined on the interval [a; b], around the x-axis is


where A(x) is the cross-sectional area at x ∈ [a, b]. Due to the construction, this is ALWAYS a circle, of radius f(x), and hence A(x) = π (f(x))2, so that


In our case, the interval of integration is infinite, and hence the integral we define is improper. Nevertheless, we find that


Hence, even though the Horn extends outward along the x-axis to ∞, the improper integral does converge, and hence there is finite volume “inside” the Horn. One can say that one can fill the Horn with π-units of a liquid. (This is oddly satisfying)
The Infinite Surface Area
The surface area of a surface of revolution is the subject. For a surface formed by revolving f(x) on [a, b] around the x-axis, the surface area is found by evaluating


This formula basically says that one can nd surface area by multiplying the circumference of the surface of evolution at x, which is a circle again, with circumference 2πf(x), by the arc-length along the original function f(x) (this is the radical part of the integrand). In our case, we get an improper integral again (call the surface area SA):


This integral is not such an easy calculation. However, we really do not need to actually calculate this quantity using an antiderivative. Instead, we make the following observation: Notice that on the interval [1;1), we have that


Thus we can say that, if


on the interval [1;1), then


by the properties of integrals. And by the Comparison Theorem for improper integrals, we can conclude that, if the integral of the smaller one (with h(x) as the integrand) diverges, then so does the integral of the larger function g(x). Indeed, we fi nd by comparison that


But we have already evaluated this last integral in class. We get


Hence this last integral diverges, and hence by comparison so does the former integral. But
this implies that the surface area of Gabriel’s Horn is infi nite!

So we have a surface with infinite surface area enclosing a finite volume.
OSCILLATORY INTEGRAL
Oscillatory integrals in one form or another have been an essential part of harmonic analysis from the very beginnings of that subject. Besides the obvious fact that the Fourier transform is itself an oscillatory integral par excellence, one need only recall the occurrence of Bessel functions in the work of Fourier, the study of asymptotic related to these functions by Airy, Stokes, and Lipschitz, and Riemann’s use of the method of “stationary phase” in finding the asymptotic of certain Fourier transforms, all of which took place well over 100 years ago.
A basic problem which comes up whenever performing a computation in harmonic analysis is how to quickly and efficiently compute (or more precisely, to estimate) an explicit integral. Of course, in some cases undergraduate calculus allows one to compute such integrals exactly, after some effort (e.g. looking up tables of special functions), but since in many applications we only need the order of magnitude of such integrals, there are often faster, more conceptual, more robust, and less computationally intensive ways to estimate these integrals.
The dyadic decomposition of a function
Littlewood–Paley theory uses a decomposition of a function f into a sum of functions fρ with localized frequencies. There are several ways to construct such a decomposition; a typical method is as follows. If f(x) is a function on R, and ρ is a measurable set (in the frequency space) with characteristic function Xρ(ξ), then fρ is defined via its Fourier transform fρ := Xρ . Informally, fρ is the piece of f whose frequencies lie in ρ. If Δ is a collection of measurable sets which (up to measure 0) are disjoint and have union on the real line, then a well behaved function f can be written as a sum of functions fρ for ρ ∈ Δ. When Δ consists of the sets of the form ρ = [-2k+1,-2k] U [2k, 2k+1] for k an integer, this gives a so-called “dyadic decomposition” of f : Σρ fρ. There are many variations of this construction; for example, the characteristic function of a set used in the definition of fρ can be replaced by a smoother function. A key estimate of Littlewood Paley theory is the Littlewood–Paley theorem, which bounds the size of the functions fρ in terms of the size of f. There are many versions of this theorem corresponding to the different ways of decomposing f. A typical estimate is to bound the Lp norm of (Σρ |fρ|2)1/2 by a multiple of the Lp norm of f. In higher dimensions it is possible to generalize this construction by replacing intervals with rectangles with sides parallel to the coordinate axes. Unfortunately these are rather special sets, which limits the applications to higher dimensions.
In the case where the integral to evaluate is non-negative, e.g.


then the method of decomposition, particularly dyadic decomposition, works quite well: split the domain of integration into natural regions, such as dyadic annuli on which a key term in the integrand is essentially constant, estimate each sub-integral (which generally reduces to the geometric problem of measuring the volume of some standard geometric set, such as the intersection of two balls), and then sum (generally one ends up with summing a standard series such a geometric series or harmonic series). For non-negative integrands, this approach tends to give answers which only differ above and below from the truth by a constant (possibly depending on things such as the dimension d). Slightly more generally, this type of estimation works well in providing upper bounds for integrals which do not oscillate very much. With some more effort, one can often extract asymptotics rather than mere upper bounds, by performing some sort of expansion (e.g. Taylor expansion) of the integrand into a main term (which can be integrated exactly, e.g. by methods from undergraduate calculus), plus an error term which can be upper bounded by an expression smaller than the final value of the main term. However, there are many cases in which one has to deal with integration of highly oscillatory integrands, in which the naive approach of taking absolute values (thus destroying most of the oscillation and cancellation) will give very poor bounds. A typical such oscillatory integral takes the form


where a is a bump function adapted to some reasonable set B (such as a ball), Φ is a real -valued phase function (usually obeying some smoothness conditions), and λ ∈ R is a parameter to measure the extent of oscillation. One could consider more general integrals in which the amplitude function a is replaced by something a bit more singular, e.g. a power singularity |x|−α, but the aforementioned dyadic decomposition trick can usually decompose such a “singular oscillatory integral” into a dyadic sum of oscillatory integrals of the above type. Also, one can use linear changes of variables to rescale B to be a normalised set, such as the unit ball or unit cube. In one dimension, the definite integral


is also of interest, where J is now an interval. While one can dyadically decompose around the endpoints of these intervals to reduce this integral to the previous smoother integral, in one dimension one can often compute the integrals more directly.


One dimensional theory
Beginning with the theory of the one-dimensional definite integrals,


where J is an interval, λ ∈ R, and Φ : J → R is a function (which we shall assume to be smooth, in order to avoid technicalities). We observe some simple invariances:
• I(−λ) = I(λ), thus negative λ and positive λ behave similarly;
• Subtracting a constant from λ does not affect the magnitude of I(λ);
• If L : R → R is any invertible affine-linear transformation, then IL(J),Φ◦L−1(λ) =| det(L)|IJ,Φ(λ).
• We haveIJ,Φ(λ) = IJ,Φ(1).From the triangle inequality we have the trivial bound |I(λ)| ≤ |J|.
This bound is of course sharp if Φ is constant. But if Φ is non-constant, we expect I(λ) to decay as λ → ±∞.


Higher dimensional theory
The higher dimensional theory is less precise than the one-dimensional theory, mainly because the structure of stationary points can be significantly more complicated. Nevertheless, we can still say quite a bit about the higher dimensional oscillatory integrals


in many cases. The van der Corput lemma becomes significantly weaker, and will not be discussed here; however, we still have the principle of non stationary phase.
Principle of non-stationary phase
Let a ∈ C0∞ (Rd), and let Φ : Rd → R be smooth such that ∇Φ is non-zero on the support of a. Then Ia,Φ(λ) =ON,a,Φ,d(λ−N) for all N ≥ 0.
Processing…Success! You're on the list.Whoops! There was an error and we couldn't process your subscription. Please reload the page and try again.Adapted from LECTURE NOTES by TERENCE TAO. No copyright infringement intended.
QUANTUM YANG–MILLS THEORY
Modern theories describe physical forces in terms of fields, e.g. the electromagnetic field, the gravitational field, and fields that describe forces between the elementary particles. A general feature of these field theories is that the fundamental fields cannot be directly measured; however, some associated quantities can be measured, such as charges, energies, and velocities. A transformation from one such field configuration to another is called a gauge transformation; the lack of change in the measurable quantities, despite the field being transformed, is a property called gauge invariance. For example, if you could measure the color of lead balls and discover that when you change the color, you still fit the same number of balls in a pound, the property of “color” would show gauge invariance. Since any kind of invariance under a field transformation is considered a symmetry, gauge invariance is sometimes called gauge symmetry. Generally, any theory that has the property of gauge invariance is considered a gauge theory.


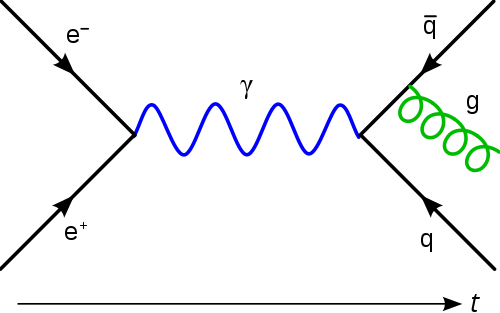
In this Feynman diagram, an electron (e–) and a positron (e+) annihilate, producing a photon (γ, represented by the blue sine wave) that becomes a quark–antiquark pair (quark q, antiquark q̄), after which the antiquark radiates a gluon (g, represented by the green helix). The idea of a gauge theory evolved from the work of Hermann Weyl. One can find in an interesting discussion of the history of gauge symmetry and the discovery of Yang–Mills theory, also known as “non-abelian gauge theory.” At the classical level one replaces the gauge group U(1) of electromagnetism by a compact gauge group G. The most important Quantum Field Theories (QFTs) for describing elementary particle physics are gauge theories. The classical example of a gauge theory is Maxwell’s theory of electromagnetism. For electromagnetism the gauge symmetry group is the abelian group U(1). If A denotes the U(1) gauge connection, locally a one-form on space-time, then the curvature or electromagnetic field tensor is the two-form F = dA, and Maxwell’s equations in the absence of charges and currents read 0 = dF = d * F. Here * denotes the Hodge duality operator; indeed, Hodge introduced his celebrated theory of harmonic forms as a generalization of the solutions to Maxwell’s equations. Maxwell’s equations describe large-scale electric and magnetic fields and also—as Maxwell discovered—the propagation of light waves, at a characteristic velocity, the speed of light.
The definition of the curvature arising from the connection must be modified to F = dA + A ^ A, and Maxwell’s equations are replaced by the Yang–Mills equations, 0 = dAF = dA* F, where dA is the gauge-covariant extension of the exterior derivative. These classical equations can be derived as variational equations from the Yang– Mills Lagrangian
L = 1/4g2 ∫ Tr F ^ F,
where Tr denotes an invariant quadratic form on the Lie algebra of G. The Yang– Mills equations are nonlinear—in contrast to the Maxwell equations. Like the Einstein equations for the gravitational field, only a few exact solutions of the classical equation are known. But the Yang–Mills equations have certain properties in common with the Maxwell equations: In particular they provide the classical description of massless waves that travel at the speed of light.
In mathematical terminology, electron phases form an Abelian group under addition, called the circle group or U(1). “Abelian” means that addition commutes, so that θ + φ = φ + θ. Group means that addition associates and has an identity element, namely “0”. Also, for every phase there exists an inverse such that the sum of a phase and its inverse is 0. Other examples of abelian groups are the integers under addition, 0, and negation, and the nonzero fractions under product, 1, and reciprocal.
Quick note

As a way of visualizing the choice of a gauge, consider whether it is possible to tell if a cylinder has been twisted. If the cylinder has no bumps, marks, or scratches on it, we cannot tell. We could, however, draw an arbitrary curve along the cylinder, defined by some function θ(x), where x measures distance along the axis of the cylinder. Once this arbitrary choice (the choice of gauge) has been made, it becomes possible to detect it if someone later twists the cylinder.
The non-abelian gauge theory of the strong force is called Quantum Chromodynamics (QCD). The use of QCD to describe the strong force was motivated by a whole series of experimental and theoretical discoveries made in the 1960s and 1970s, involving the symmetries and high-energy behavior of the strong interactions. But classical nonabelian gauge theory is very different from the observed world of strong interactions; for QCD to describe the strong force successfully, it must have at the quantum level the following three properties, each of which is dramatically different from the behavior of the classical theory:
- It must have a “mass gap;” namely there must be some constant Δ > 0 such that every excitation of the vacuum has energy at least Δ.
- It must have “quark confinement,” that is, even though the theory is described in terms of elementary fields, such as the quark fields, that transform non-trivially under SU(3), the physical particle states—such as the proton, neutron, and pion—are SU(3)-invariant.
- It must have “chiral symmetry breaking,” which means that the vacuum is potentially invariant (in the limit, that the quark-bare masses vanish) only under a certain subgroup of the full symmetry group that acts on the quark fields.
The first point is necessary to explain why the nuclear force is strong but short-ranged; the second is needed to explain why we never see individual quarks; and the third is needed to account for the “current algebra” theory of soft pions that was developed in the 1960s. Both experiment—since QCD has numerous successes in confrontation with experiment—and computer simulations, carried out since the late 1970s, have given strong encouragement that QCD does have the properties cited above. These properties can be seen, to some extent, in theoretical calculations carried out in a variety of highly oversimplified models (like strongly coupled lattice gauge theory). But they are not fully understood theoretically; there does not exist a convincing, whether or not mathematically complete, theoretical computation demonstrating any of the three properties in QCD, as opposed to a severely simplified truncation of it.
The Problem
To establish existence of four-dimensional quantum gauge theory with gauge group G, one should define a quantum field theory (in the above sense) with local quantum field operators in correspondence with the gauge-invariant local polynomials in the curvature F and its covariant derivatives, such as Tr FijFkl(x). Correlation functions of the quantum field operators should agree at short distances with the predictions of asymptotic freedom and perturbative renormalization theory, as described in textbooks. Those predictions include among other things the existence of a stress tensor and an operator product expansion, having prescribed local singularities predicted by asymptotic freedom. Since the vacuum vector Ω is Poincar´e invariant, it is an eigenstate with zero energy, namely HΩ = 0. The positive energy axiom asserts that in any quantum field theory, the spectrum of H is supported in the region [0,∞). A quantum field theory has a mass gap Δ if H has no spectrum in the interval (0, Δ) for some Δ > 0. The supremum of such Δ is the mass m, and we require m < ∞.Yang–Mills Existence and Mass Gap. Prove that for any compact simple gauge group G, a non-trivial quantum Yang–Mills theory exists on R4 and has a mass gap Δ > 0.
Mathematical Perspective
Wightman and others have questioned for approximately fifty years whether mathematically well-defined examples of relativistic, nonlinear quantum field theories exist. We now have a partial answer: Extensive results on the existence and physical properties of nonlinear QFTs have been proved through the emergence of the body of work known as “constructive quantum field theory” (CQFT). The answers are partial, for in most of these field theories one replaces the Minkowski space-time M4 by a lower-dimensional space-time M2 or M3, or by a compact approximation such as a torus. (Equivalently in the Euclidean formulation one replaces Euclidean space-time R4 by R2 or R3.) Some results are known for Yang Mills theory on a 4-torus T4 approximating R4, and, while the construction is not complete, there is ample indication that known methods could be extended to construct Yang–Mills theory on T4. In fact, at present we do not know any non-trivial relativistic field theory that satisfies the Wightman (or any other reasonable) axioms in four dimensions. So even having a detailed mathematical construction of Yang–Mills theory on a compact space would represent a major breakthrough. Yet, even if this were accomplished, no present ideas point the direction to establish the existence of a mass gap that is uniform in the volume. Nor do present methods suggest how to obtain the existence of the infinite volume limit T4 ➜ R4.
Processing…Success! You're on the list.Whoops! There was an error and we couldn't process your subscription. Please reload the page and try again.GYROID
A gyroid structure is a distinct morphology that is triply periodic and consists of minimal iso-surfaces containing no straight lines.
The gyroid was discovered in 1970 by Alan Schoen, a NASA crystallographer interested in strong but light materials. Among its most curious properties was that, unlike other known surfaces at the time, the gyroid contains no straight lines or planar symmetry curves. In 1975, Bill Meeks discovered a 5-parameter family of embedded genus 3 triply periodic minimal surfaces.
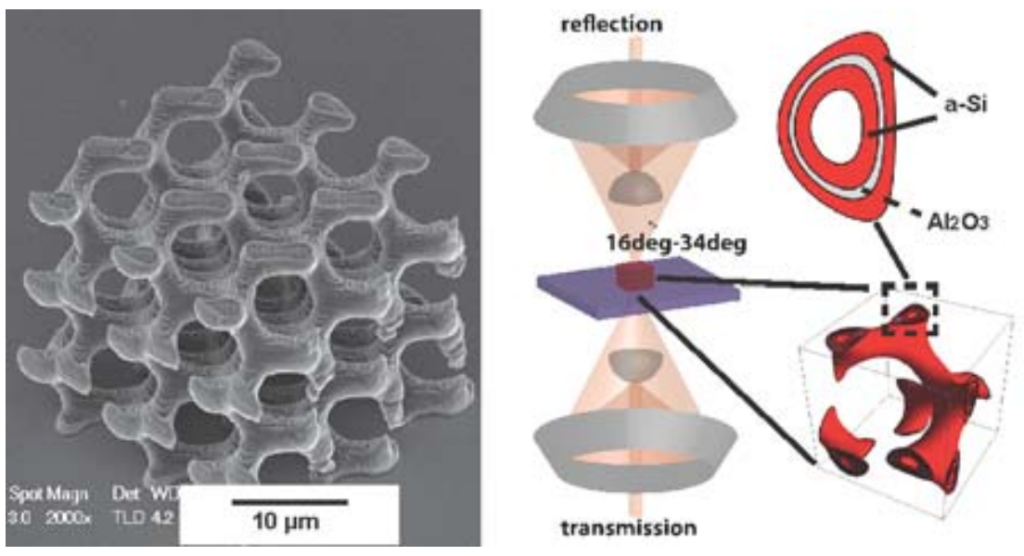
Photonic crystals were synthesized by deposition of a-Si/Al2O3 coatings onto a sacrificial polymer scaffold defined by two-photon lithography. We observed a 100% reflectance at 7.5 µm for single gyroids with a unit cell size of 4.5 µm, in agreement with the photonic bandgap position predicted from full-wave electromagnetic simulations, whereas the observed reflection peak shifted to 8 µm for a 5.5 µm unit cell size. This approach represents a simulation-fabrication-characterization platform to realize three dimensional gyroid photonic crystals with well-defined dimensions in real space and tailored properties in momentum space.


Three-dimensional photonic crystals offer opportunities to probe interesting photonic states such as bandgaps, Weyl points, well-controlled dislocations and defects. Combinations of morphologies and dielectric constants of materials can be used to achieve desired photonic states. Gyroid crystals have interesting three-dimensional morphologies defined as triply periodic body centered cubic crystals with minimal surfaces containing no straight lines. A single gyroid structure consists of iso-surfaces described by sin(x)cos(y) + sin(y)cos(z) + sin(z)cos(x) > u(x, y, z), where the surface is constrained by u(x, y, z). Gyroid structures exist in biological systems in nature. For example, self-organizing process of biological membranes forms gyroid photonic crystals that exhibit the iridescent colors of butterfly’s wings. Optical properties of gyroids could vary with tuning of u(x, y, z), unit cell size, spatial symmetry as well as refractive index contrast. Single gyroid photonic crystals, when designed with high refractive index and fill fraction, are predicted to possess among the widest complete three-dimensional bandgaps, making them interesting for potential device applications such as broadband filters and optical cavities.
Gyroid representation
The minimal surface of the gyroid can be approximated by the level set equation, with the iso-value, h, set to h = 0. The parameter, a, is the unit cell length. By selecting alternative values for h between the limits (±1.413), the surface can be offset along its normal direction; beyond those limits the surface becomes disconnected, and ceases to exist for |h| > 1.5. Introducing an inequality enables the selection of the regions to either side of the shifted surface, producing the solid-network form. The solid-surface form is generated by selecting the region between two surfaces shifted along the surface normal to either side from their gyroid mid-surface (or alternatively using the inequality. The inequality produces two interwoven non-connected solid-network forms.


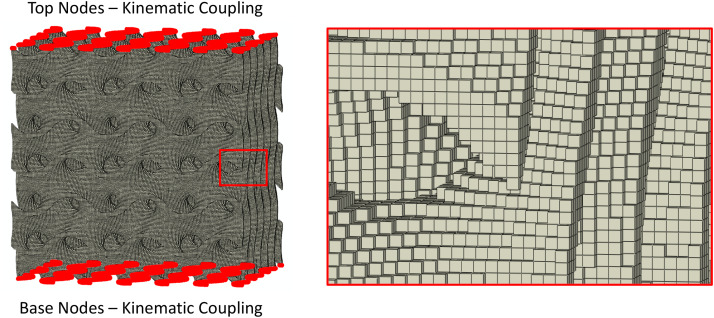
Solid finite element model


A voxel based finite element (FE) mesh with eight-node hexahedral elements was generated to approximate the solid-surface gyroid within a cubic bulk form. Firstly, a triangular mesh was constructed within Matlab using the iso-surface for h = 0. This mesh was copied and translated along the local normal to create the thickened solid-surface geometry and enclosed at the boundary edges. A voxelization function was then used to produce the voxel mesh. The voxel element size was set to target a minimum of 4 elements through the thickness direction.
Processing…Success! You're on the list.Whoops! There was an error and we couldn't process your subscription. Please reload the page and try again.Banach–Tarski Paradox
The Banach–Tarski paradox is a theorem in set-theoretic geometry, which states the following: Given a solid ball in 3‑dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball. Indeed, the reassembly process involves only moving the pieces around and rotating them without changing their shape. However, the pieces themselves are not “solids” in the usual sense, but infinite scatterings of points. The reconstruction can work with as few as five pieces.
Dissection and reassembly of a figure is an important concept in classical geometry. It was used extensively by the Greeks to derive theorems about area, including the well-known Pythagorean Theorem.


Any two polygons with the same area are congruent by dissection
Proof-
First, observe that congruence by dissection is an equivalence relation. To see transitivity, suppose that a polygon Q can be dissected along some set of cuts into pieces that can be rearranged to form P, and can also be dissected along another set of cuts into pieces that form R. Then by making both sets of cuts, we end up with a set of pieces that can be rearranged to form either P or R; composing these two procedures, we get that P and R are congruent by dissection. Now it is sufficient to show that every polygon is congruent by dissection to a square. To do this, dissect the polygon into triangles. Each of these triangles is easily dissected into a rectangle, and then into a square.
Lebesgue Measure


In order to formalize our notions of length, area, and volume, we want a definition of measure that assigns nonnegative reals (or ∞) to subsets of Rn, with the following properties.
An n-dimensional hypercube of side x has measure xn.
The measure of the union of finitely many disjoint figures Ai ⊆ Rn is the sum of their measures. (One could also ask for countable additivity instead of just finite additivity, but we will not consider such cases here.)
One such definition is the Lebesgue measure (which is in fact countably additive). However, there is a serious caveat: it will turn out that it is not defined for all sets. The construction of the Lebesgue measure is somewhat technical; one definition is as follows.
For any subset B ⊆ R2, define λ∗(B) to be the infimum of all k ∈ [0,∞] such that B can covered by a countable set of hypercubes with total measure k. Then we say that A ⊆ R2 is Lebesgue measurable if λ∗(B) = λ∗(A ∩ B) + λ∗(B r A) for all B ⊆ Rn; if so, its Lebesgue measure is defined to be λ(A) = λ∗(A).
Construction of the Paradox


By Qef – Paradoxical decomposition F2.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=36559803 Our goal is to show that the unit ball B3 is equi-decomposable with two unit balls under the isometry group of R3 . We will show how to do this for a spherical shell S 2 . Then we can view most of the ball as a collection of spherical shells of radii 0 < r < 1, and apply the same transformations to each shell. This lets us take care of every point except the center. Our first task, then, is to show how to remove the center.
Lemma- B3 is equi-decomposable with B3 r {0}, where 0 is the ball’s center.
Proof. Consider a small circle that passes through 0 and is contained entirely in B3. Let ρ be a 1-radian rotation of this circle. Then the points 0, ρ0, ρ20, ρ30, . . . are distinct, and if we apply ρ to just this set of points, we get the same set except with 0 missing. This yields a two-piece equi-decomposition of B3 with B3 r {0}: one piece is {0, ρ0, ρ20, ρ30, . . . } going to {ρ0, ρ20, ρ30, . . . } under the rotation ρ, and the other d piece is the rest of the ball going to itself.
Theorem (Banach-Tarski Paradox) The unit ball B3 is equi-decomposable with two copies of itself.
Proof. We see that S 2 is equi-decomposable with two copies of itself. Scaling this construction about the center allows us to do this for the spherical shells of radius r, for any 0 < r < 1, with the same rotations. If we do this for all these shells simultaneously, we get an equi-decomposition of B3 r{0} with two copies of itself. Finally, we see that B3 is equi-decomposable with two copies of itself.
With some care, it can be shown that this equi-decomposition can be carried out using just five pieces. Somehow, making some cuts with the Axiom of Choice has allowed us to completely subvert the intuitive properties of volume. As promised, it is now a simple extension to equi-decompose any two bounded sets with nonempty interior.
At first glance, the Banach-Tarski Paradox appears to be an actual contradiction with measure theory, for if we measure all the pieces used in the construction, they must add up both to the volume of the ball and to twice the volume of the ball, and these are different positive real numbers. The resolution of this paradox is that the pieces must not be Lebesgue measurable—or more generally, any function that satisfies the properties of measure listed above cannot be defined on these piece.
Processing…Success! You're on the list.Whoops! There was an error and we couldn't process your subscription. Please reload the page and try again.CHAOS THEORY
Chaos theory is a branch of mathematics focusing on the study of chaos states of dynamical systems whose apparently random states of disorder and irregularities are often governed by deterministic laws that are highly sensitive to initial conditions. When employing mathematical theorems, one should remain careful about whether their hypotheses are valid within the frame of the questions considered. Among such hypotheses in the domain of dynamics, a central one is the continuity of time and space (that an infinity of points exists between two points). This hypothesis, for example, may be invalid In the cognitive neurosciences of perception, where a finite time threshold often needs to be considered.
Birth of the chaos theory
Poincaré and phase space
With the work of Laplace, the past and the future of the solar system could be calculated and the precision of this calculation depended on the capacity to know the initial conditions of the system, a real challenge for “geometricians,” as alluded to by d’Holbach and Le Verrier. Henri Poincaré developed another point of view, as follows: in order to study the evolution of a physical system over time, one has to construct a model based on a choice of laws of physics and to list the necessary and sufficient parameters that characterize the system (differential equations are often in the model). One can define the state of the system at a given moment, and the set of these system states is named phase space.
The phenomenon of sensitivity to initial conditions was discovered by Poincaré in his study of the the n-body problem, then by Jacques Hadamard using a mathematical model named geodesic flow, on a surface with a nonpositive curvature, called Hadamard’s billards. A century after Laplace, Poincaré indicated that randomness and determinism become somewhat compatible because of the long-erm unpredictability.
A very small cause, which eludes us, determines a considerable effect that we cannot fail to see, and so we say that this effect Is due to chance. If we knew exactly the laws of nature and the state of the universe at the initial moment, we could accurately predict the state of the same universe at a subsequent moment. But even If the natural laws no longer held any secrets for us, we could still only know the state approximately. If this enables us to predict the succeeding state to the same approximation, that is all we require, and we say that the phenomenon has been predicted, that It Is governed by laws. But this is not always so, and small differences in the initial conditions may generate very large differences in the final phenomena. A small error in the former will lead to an enormous error In the latter. Prediction then becomes impossible, and we have a random phenomenon.
This was the birth of chaos theory.


Lorenz and the butterfly effect Rebirth of chaos theory
Edward Lorenz, from the Massachusetts Institute of Technology (MIT) is the official discoverer of chaos theory. He first observed the phenomenon as early as 1961 and, as a matter of irony, he discovered by chance what would be called later the chaos theory, in 1963, while making calculations with uncontrolled approximations aiming at predicting the weather. The anecdote is of interest: making the same calculation rounding with 3-digit rather than 6-digit numbers did not provide the same solutions; indeed, in nonlinear systems, multiplications during iterative processes amplify differences in an exponential manner. By the way, this occurs when using computers, due to the limitation of these machines which truncate numbers, and therefore the accuracy of calculations.
Lorenz considered, as did many mathematicians of his time, that a small variation at the start of a calculation would Induce a small difference In the result, of the order of magnitude of the initial variation. This was obviously not the case, and all scientists are now familiar with this fact. In order to explain how important sensitivity the to initial conditions was, Philip Merilees, the meteorologist who organized the 1972 conference session where Lorenz presented his result, chose himself the title of Lorenz’s talk, a title that became famous: “Predictability: does the flap of a butterfly’s wing in Brazil set off a tornado in Texas?” This title has been cited and modified in many articles, as humorously reviewed by Nicolas Witkowski. Lorenz had rediscovered the chaotic behavior of a nonlinear system, that of the weather, but the term chaos theory was only later given to the phenomenon by the mathematician James A. Yorke, in 1975. Lorenz also gave a graphic description of his findings using his computer. The figure that appeared was his second discovery: the attractors.
The golden age of chaos theory
Felgenbaum and the logistic map
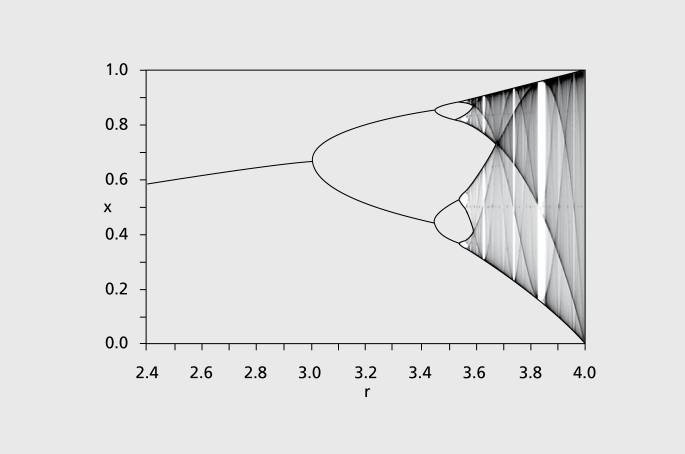
Mitchell Jay Feigenbaum proposed the scenario called period doubling to describe the transition between a regular dynamics and chaos. His proposal was based on the logistic map introduced by the biologist Robert M. May in 1976. While so far there have been no equations this text, I will make an exception to the rule of explaining physics without writing equations, and give here a rather simple example. The logistic map is a function of the segment [0,1] within itself defined by:
xn+1=rxn(1-xn)
where n = 0, 1, … describes the discrete time, the single dynamical variable, and 0≤r≤4 is a parameter. The dynamic of this function presents very different behaviors depending on the value of the parameter r:
For 0≤r≤3, the system has a fixed point attractor that becomes unstable when r=3.
Pour 3<r<3,57…, the function has a periodic orbit as attractor, of a period of 2n where n is an integer that tends towards infinity when r tends towards 3,57…
When r=3,57…, the function then has a Feigenbaum fractal attractor.
When over the value of r=4, the function goes out of the interval [0,1]


COURTESY- Christian Oestreicher, Department of Public Education, State of Geneva, Switzerland;* E-mail:hc.eg.ude@rehciertseo.naitsirhc
KNOT THEORY
In topology, knot theory is the study of mathematical knots. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3 (in topology, a circle isn’t bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
Although people have been making use of knots since the dawn of our existence, the actual mathematical study of knots is relatively young, closer to 100 years than 1000 years. In contrast, Euclidean geometry and number theory, which have been studied over a considerable number of years, germinated because of the cultural “pull” and the strong effect that calculations and computations generated. It is still quite common to see buildings with ornate knot or braid lattice-work. However, as a starting point for a study of the mathematics of a knot, we need to excoriate this aesthetic layer and concentrate on the shape of the knot. Knot theory, in essence, is the study of the geometrical aspects of these shapes. Not only has knot theory developed and grown over the years in its own right, but also the actual mathematics of knot theory has been shown to have applications in various branches of the sciences, for example, physics, molecular biology, chemistry.
FUNDAMENTAL CONCEPTS OF KNOT THEORY
A knot, succinctly, is an entwined circle. However, throughout this book we shall think of a knot as an entwined polygon in 3-dimensional space. The reason for this is that it allows us, with recourse to combinatorial topology, 1 to exclude wild knots. Close to the point P, in a sense we may take this to be a “limit” point, the knot starts to cluster together in a concertina fashion. Therefore, in the vicinity of such a point particular care needs to be taken with the nature of the knots. We shall not in this exposition apply or work within the constraints of such (wild) knots. In fact, since wild knots axe not that common, this will be the only reference to these kind of knots. Therefore, in order to avoid the above peculiarity, we shall assume, without exception, everything that follows is considered from the standpoint of combinatorial topology. As mentioned in the preface, our intention is to avoid as ,much as possible mathematical argot and to concentrate on the substance and application of knot theory. Infrequently, as above, it will be necessary, in order to underpin an assumption, to introduce such a piece of mathematical argot. Again, as mentioned in the preface, knowledge of such concepts will not usually be required to be able to understand what follows.


Definition. On a given knot K we may perform the following four operations.
(1) We may divide an edge, AB, in space of K into two edges, AC, CB, by placing a point C on the edge AB.
(1)’ [The converse of (1)] If AC and CB are two adjacent edges of K such that if C is erased AB becomes a straight line, then we may remove the point C.
(2) Suppose C is a point in space that does not lie on K. If the triangle ABC, formed by AB and C, does not intersect K, with the exception of the edge AB, then we may remove AB and add the two edges AC and CB.
(2)’ [The converse of (2)] If there exists in space a triangle ABC that contains two adjacent edges AC and CB of K, and this triangle does not intersect K, except at the edges AC and CB, then we may delete the two edges AC, CB and add the edge AB.




These four operations (1), (1)’, (2) and (2)’ are called the elementary knot moves.
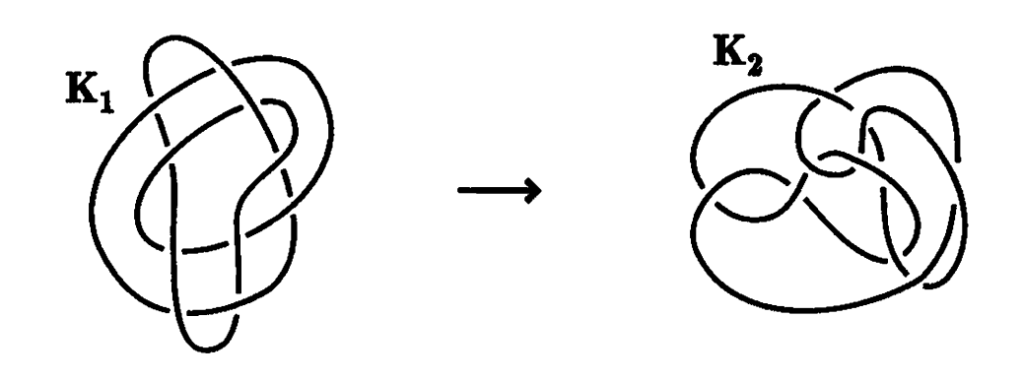
A knot is not perceptively changed if we apply only one elementary knot move. However, if we repeat the process at different places, several times, then the resultant knot seems to be a completely different knot. For example, let us look at the two knots K1 and K2 which may be called Perko’s pair.


In appearance Perko’s pair of knots looks completely different. In fact, for the better part of 100 years, nobody thought otherwise. However, it is possible to change the knot K1 into the knot K2 by performing the elementary knot moves a significant number of times. This was only shown in 1970 by the American lawyer K.A. Perko. Knots that can be changed from one to the other by applying the elementary knot move are said to be equivalent or equal. Therefore, the two knots are equivalent.
Processing…Success! You're on the list.Whoops! There was an error and we couldn't process your subscription. Please reload the page and try again.Poincaré Conjecture
If we stretch a rubber band around the surface of an apple, then we can shrink it down to a point by moving it slowly, without tearing it and without allowing it to leave the surface. On the other hand, if we imagine that the same rubber band has somehow been stretched in the appropriate direction around a doughnut, then there is no way of shrinking it to a point without breaking either the rubber band or the doughnut. We say the surface of the apple is “simply connected,” but that the surface of the doughnut is not. Poincaré, almost a hundred years ago, knew that a two dimensional sphere is essentially characterized by this property of simple connectivity, and asked the corresponding question for the three dimensional sphere.
Clay Mathematics InstitutePROBLEM STATEMENT
If a compact three-dimensional manifold M3 has the property that every simple closed curve within the manifold can be deformed continuously to a point, does it follow that M3 is homeomorphic to the sphere S3?
Henri Poincare’ commented, with considerable foresight, “Mais cette question nous entraˆınerait trop loin”. Since then, the hypothesis that every simply connected closed 3-manifold is homeomorphic to the 3-sphere has been known as the Poincare’ Conjecture. It has inspired topologists ever since, and attempts to prove it have led to many advances in our understanding of the topology of manifolds. From the first, the apparently simple nature of this statement has led mathematicians to overreach. Four years earlier, in 1900, Poincare’ himself had been the first to err, stating a false theorem that can be phrased as follows.
HIGHER DIMENSIONS
The fundamental group plays an important role in all dimensions even when it is trivial, and relations between generators of the fundamental group correspond to two-dimensional disks, mapped into the manifold. In dimension 5 or greater, such disks can be put into general position so that they are disjoint from each other, with no self-intersections, but in dimension 3 or 4 it may not be possible to avoid intersections, leading to serious difficulties. Stephen Smale announced a proof of the Poincare’ Conjecture in high dimensions in 1960. He was quickly followed by John Stallings, who used a completely different method, and by Andrew Wallace, who had been working along lines quite similar to those of Smale.
The Ricci Flow


Let M be an n-dimensional complete Riemannian manifold with the Riemannian metric gij . The Levi-Civita connection is given by the Christoffel symbols


where gij is the inverse of gij . The summation convention of summing over repeated indices is used here and throughout the book. The Riemannian curvature tensor is given by


We lower the index to the third position, so that


The curvature tensor Rijkl is anti-symmetric in the pairs i, j and k, l and symmetric in their interchange:


Also the first Bianchi identity holds


The Ricci tensor is the contraction


and the scalar curvature is


We denote the covariant derivative of a vector field v = vj (∂/∂xj)by


and of a 1-form by


These definitions extend uniquely to tensors so as to preserve the product rule and contractions. For the exchange of two covariant derivatives, we have


and similar formulas for more complicated tensors. The second Bianchi identity is given by


For any tensor T = Tijk we define its length by


and we define its Laplacian by


the trace of the second iterated covariant derivatives. Similar definitions hold for more general tensors.
The Ricci flow of Hamilton is the evolution equation


for a family of Riemannian metrics gij (t) on M. It is a nonlinear system of second order partial differential equations on metrics.
In August 2006, Grigory Perelman was offered the Fields Medal for “his contributions to geometry and his revolutionary insights into the analytical and geometric structure of the Ricci flow”, but he declined the award, stating: “I’m not interested in money or fame; I don’t want to be on display like an animal in a zoo.” On 22 December 2006, the scientific journal Science recognized Perelman’s proof of the Poincaré conjecture as the scientific “Breakthrough of the Year”, the first such recognition in the area of mathematics.