

MIRROR SYMMETRY
With the appreciation of the importance of Yang–Mills gauge theories in describing the physics of particle interactions, and with the appreciation of its importance in the mathematics of vector bundles, renewed interaction between the two fields began to take place. For example, the importance of instantons and monopoles came to be appreciated from both the physical and mathematical points of view. With the discovery of supersymmetry and its logical completion to superstring theory, a vast arena of interaction opened up between physics and mathematics and continues today at a very deep level for both fields. Mathematicians and physicists often find it difficult to discuss their work and interact with each other. The reason for this appears to be twofold. First, the languages used in the two fields are rather different. This problem is gradually being resolved as we recognize the need to become “bilingual.” The second and more serious problem is that the established scientific methods in the two fields do not converge. Whereas mathematics places emphasis on rigorous foundations and the interplay of various structures, to a physicist the relevant aspects are physical clarity and physical interconnection of ideas, even if they come at the cost of some mathematical rigor. This can lead to friction between mathematicians and physicists.

Generally Speaking…
Mirror symmetry is an example of a general phenomenon known as duality, which occurs when two seemingly different physical systems are isomorphic in a non-trivial way. The non-triviality of this isomorphism involves the fact that quantum corrections must be taken into account. Mathematically, a good analogy is the Fourier transform, where local concepts such as products are equivalent to convolution products, requiring integration over the whole space. Thus it is difficult to understand such isomorphisms in the classical context. In particular, under such an isomorphism, certain complicated quantities involving quantum corrections in one system get mapped to simple classical questions in the other. Thus, finding such dualities leads to solving complicated physical questions in terms of simple ones in the dual theory. Precisely for this reason the discovery of duality symmetries has revolutionized our understanding of quantum theories and string theory.
Strings and Compactification

In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. These strings look like small segments or loops of ordinary string. String theory describes how strings propagate through space and interact with each other. On distance scales larger than the string scale, a string will look just like an ordinary particle, with its mass, charge, and other properties determined by the vibrational state of the string.
There are notable differences between the world described by string theory and the everyday world. In everyday life, there are three familiar dimensions of space (up/down, left/right, and forward/backward), and there is one dimension of time (later/earlier). Thus, in the language of modern physics, one says that spacetime is four-dimensional. One of the peculiar features of string theory is that it requires extra dimensions of spacetime for its mathematical consistency. In superstring theory, the version of the theory that incorporates a theoretical idea called supersymmetry, there are six extra dimensions of spacetime in addition to the four that are familiar from everyday experience.
Lets Talk About…
1. Manifolds
We describe a manifold by coordinate charts. Let {Uα} be an open covering of the topological space M. We endow M with the structure of an n-dimensional manifold with the following information. Let ϕα : Uα ➥ Rn be a coordinate chart (one may think of coordinates xα = (xα)i , i = 1, …, n as representing the points themselves, i.e., their pre-images under ϕα). On Uα ∩ Uβ, we can relate coordinates (xα) to coordinates (xβ) by xα = ϕα ◦ ϕβ-1(xβ).
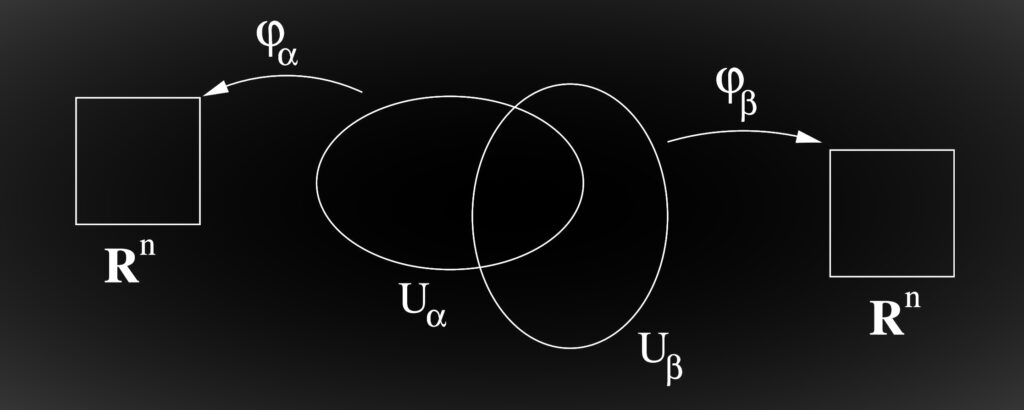

The map gαβ = ϕα ◦ ϕβ−1 is a transition function. Note that gαβ = gβα−1 and gαβ gβγ gγα = 1. As an alternative to this structure, we could form a manifold based solely on the data of patches and transition functions satisfying the above relations. A manifold is called “differentiable” if its transition functions are differentiable, and “smooth” if the transition functions are smooth (C∞). If n = 2k and one can (and does) choose ϕα : Uα ➥ Ck with holomorphic transition functions, the manifold is called “complex.” Note that this extra structure is restrictive. Two complex manifolds may be diffeomorphic as real manifolds (meaning there are invertible, onto, differentiable maps between the two), but there may be no complex analytic mapping between them (we then say they have different complex structures). Likewise, two homeomorphic manifolds may have different structures as differentiable manifolds. Differentiability depends on the coordinate chart maps ϕα.
2. Vector Bundles
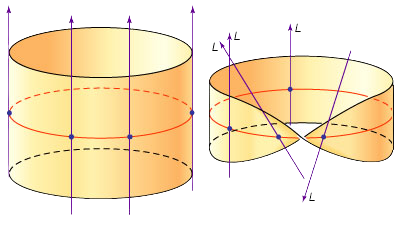
Vector bundles are constructed similarly, only now every point carries an additional structure of a vector space (“fiber”) over it. Clearly, by retaining the information of the point but forgetting the information of the vector space, we get a map to the underlying manifold. From the description above, it is clear that the simplest vector bundle, E, will be a product space E = M × V, where M is a manifold and V is an r-dimensional vector space. E is said to be a rank r vector bundle. E is equipped with the map π : E → M, namely π((m, v)) = m. Such a vector bundle is called “trivial.” Locally, all vector bundles are trivial and look like products. So a rank r vector bundle E is a smooth manifold with a map π : E → M to a base manifold, M, such that every point x ∈ M has a neighborhood x ∈ Ux with π−1(Ux) ∼= Ux × Rr.

Algebraic Geometry
Algebraic geometry deals with curves or surfaces (or more abstract generalizations of these) which can be viewed both as geometric objects and as solutions of algebraic (specifically, polynomial) equations. Algebraic geometry sets out to answer these questions by applying the techniques of abstract algebra to the set of polynomials that define the curves (which are then called “algebraic varieties”). The mathematics involved is inevitably quite hard, although it is covered in degree-level courses. Other common questions in algebraic geometry concern points of special interest such as singularities, inflection points and points at infinity – we shall see these throughout the catalogue. More advanced questions in algebraic geometry concern relations between curves given by different equations and the topology of curves, and many other topics.
CLICK THE LINK TO KNOW MORE ABOUT Algebraic Geometry.


Calabi–Yau Manifolds
Compactification can be used to construct models in which spacetime is effectively four-dimensional. However, not every way of compactifying the extra dimensions produces a model with the right properties to describe nature. In a viable model of particle physics, the compact extra dimensions must be shaped like a Calabi–Yau manifold. A Calabi Yau manifold is a special space which is typically taken to be six-dimensional in applications to string theory. It is named after mathematicians Eugenio Calabi and Shing-Tung Yau.
After Calabi–Yau manifolds had entered physics as a way to compactify extra dimensions, many physicists began studying these manifolds. Lance Dixon, Wolfgang Lerche, Cumrun Vafa, and Nick Warner noticed that given such a compactification of string theory, it is not possible to reconstruct uniquely a corresponding Calabi–Yau manifold. Instead, two different versions of string theory called type IIA string theory and type IIB can be compactified on completely different Calabi–Yau manifolds giving rise to the same physics. In this situation, the manifolds are called mirror manifolds, and the relationship between the two physical theories is called mirror symmetry.
Homological Mirror Symmetry
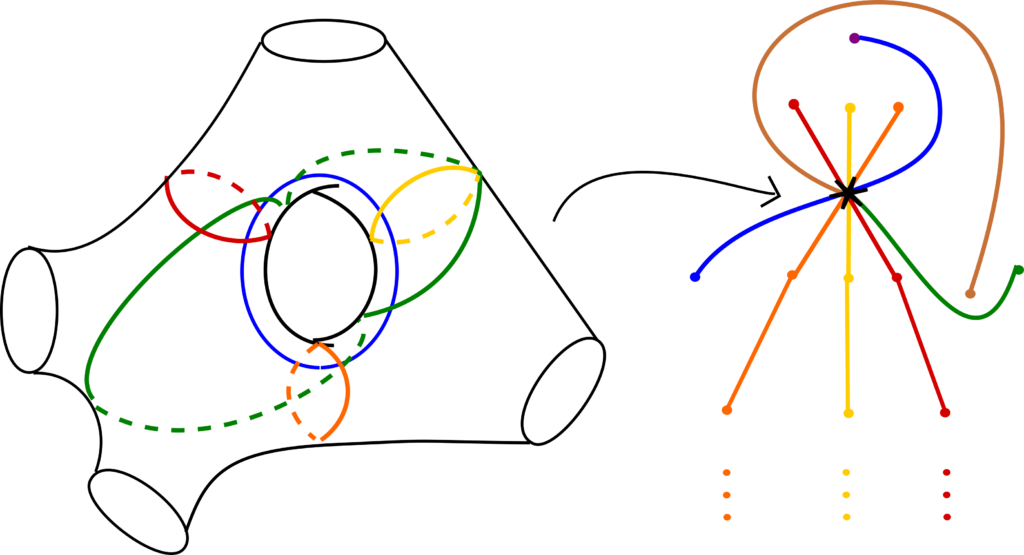

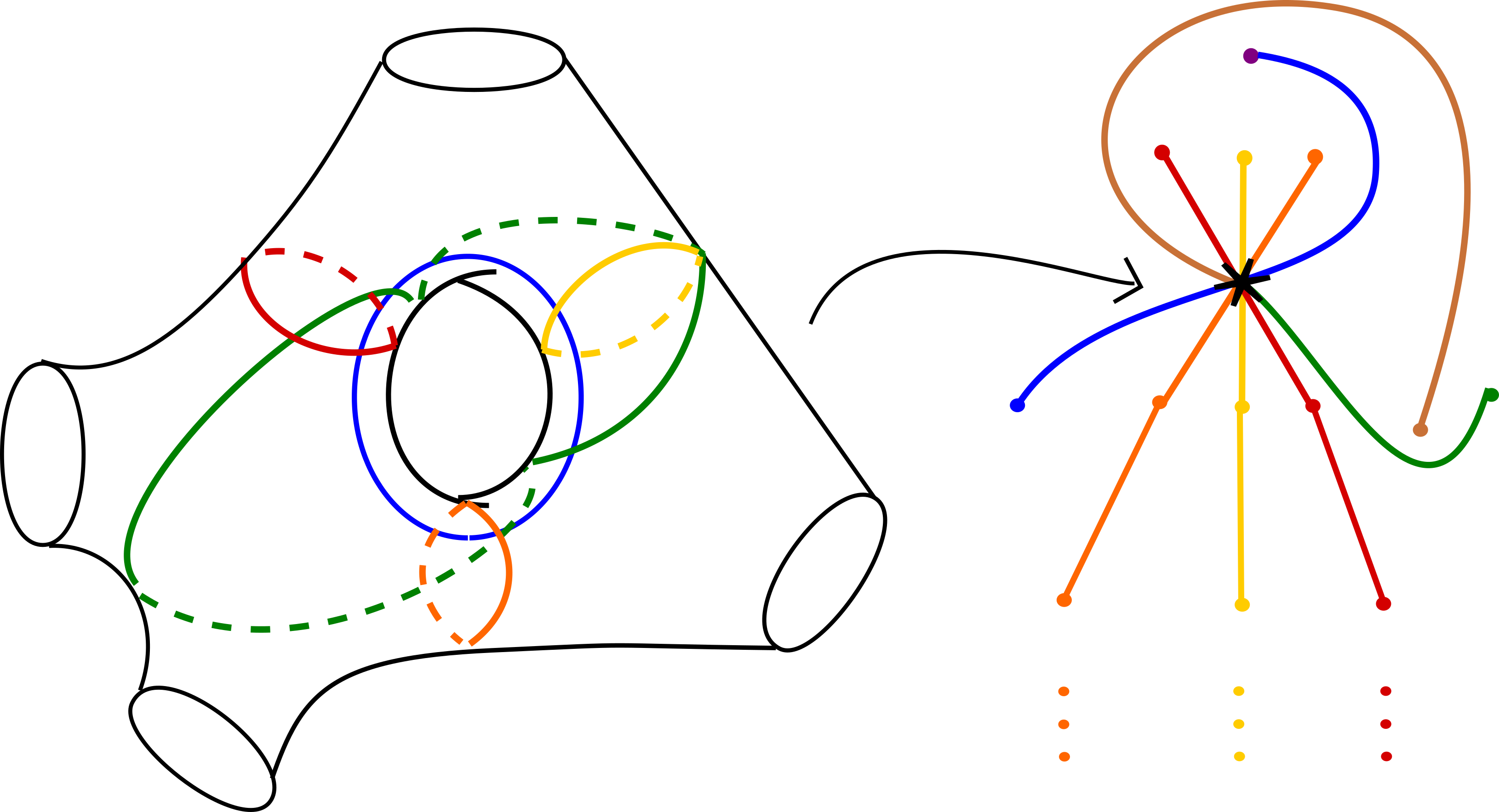
In string theory and related theories in physics, a brane is a physical object that generalizes the notion of a point particle to higher dimensions. For example, a point particle can be viewed as a brane of dimension zero, while a string can be viewed as a brane of dimension one. It is also possible to consider higher-dimensional branes. The word brane comes from the word “membrane” which refers to a two-dimensional brane. In string theory, a string may be open (forming a segment with two endpoints) or closed (forming a closed loop). D-branes are an important class of branes that arise when one considers open strings. As an open string propagates through spacetime, its endpoints are required to lie on a D-brane. The letter “D” in D-brane refers to a condition that it satisfies, the Dirichlet boundary condition. Mathematically, branes can be described using the notion of a category. This is a mathematical structure consisting of objects, and for any pair of objects, a set of morphisms between them. In most examples, the objects are mathematical structures (such as sets, vector spaces, or topological spaces) and the morphisms are functions between these structures. One can also consider categories where the objects are D-branes and the morphisms between two branes α and β are states of open strings stretched between α and β. In the B-model of topological string theory, the D-branes are complex submanifolds of a Calabi–Yau together with additional data that arise physically from having charges at the endpoints of strings. Intuitively, one can think of a submanifold as a surface embedded inside the Calabi–Yau, although submanifolds can also exist in dimensions different from two. In mathematical language, the category having these branes as its objects is known as the derived category of coherent sheaves on the Calabi–Yau. In the A-model, the D-branes can again be viewed as submanifolds of a Calabi–Yau manifold. Roughly speaking, they are what mathematicians call special Lagrangian submanifolds. This means among other things that they have half the dimension of the space in which they sit, and they are length-, area-, or volume-minimizing. The category having these branes as its objects is called the Fukaya category.
SYZ conjecture
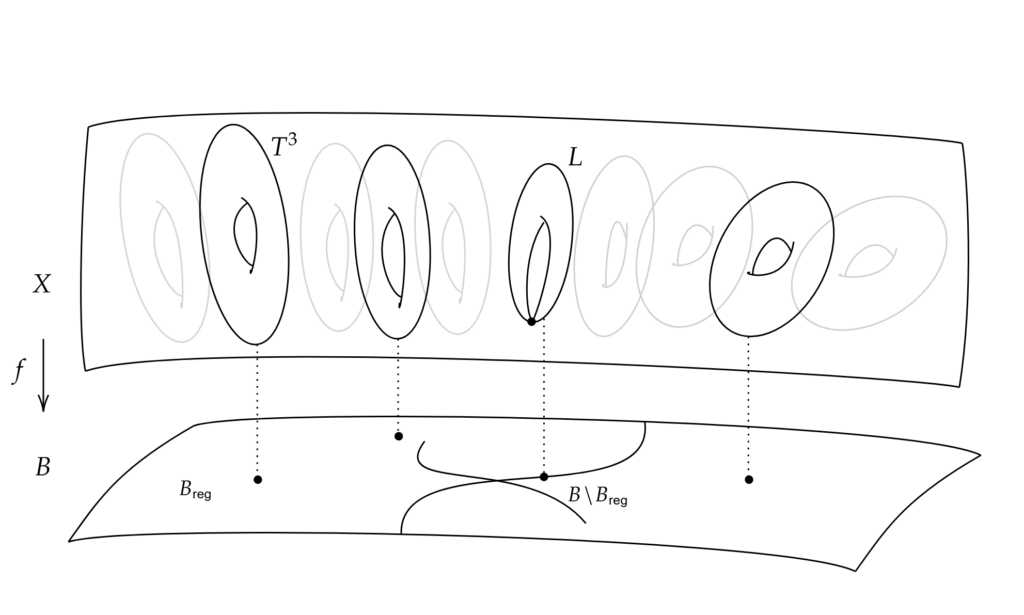

The SYZ conjecture is an attempt to understand the mirror symmetry conjecture, an issue in theoretical physics and mathematics. The original conjecture was proposed in a paper by Strominger, Yau, and Zaslow, entitled “Mirror Symmetry is T-duality”. Along with the homological mirror symmetry conjecture, it is one of the most explored tools applied to understand mirror symmetry in mathematical terms. While the homological mirror symmetry is based on homological algebra, the SYZ conjecture is a geometrical realization of mirror symmetry.
The initial proposal of the SYZ conjecture by Strominger, Yau, and Zaslow, was not given as a precise mathematical statement. One part of the mathematical resolution of the SYZ conjecture is to, in some sense, correctly formulate the statement of the conjecture itself. There is no agreed upon precise statement of the conjecture within the mathematical literature, but there is a general statement that is expected to be close to the correct formulation of the conjecture, which is presented here. This statement emphasizes the topological picture of mirror symmetry, but does not precisely characterize the relationship between the complex and symplectic structures of the mirror pairs, or make reference to the associated Riemannian metrics involved.



