QUANTUM YANG–MILLS THEORY
Modern theories describe physical forces in terms of fields, e.g. the electromagnetic field, the gravitational field, and fields that describe forces between the elementary particles. A general feature of these field theories is that the fundamental fields cannot be directly measured; however, some associated quantities can be measured, such as charges, energies, and velocities. A transformation from one such field configuration to another is called a gauge transformation; the lack of change in the measurable quantities, despite the field being transformed, is a property called gauge invariance. For example, if you could measure the color of lead balls and discover that when you change the color, you still fit the same number of balls in a pound, the property of “color” would show gauge invariance. Since any kind of invariance under a field transformation is considered a symmetry, gauge invariance is sometimes called gauge symmetry. Generally, any theory that has the property of gauge invariance is considered a gauge theory.


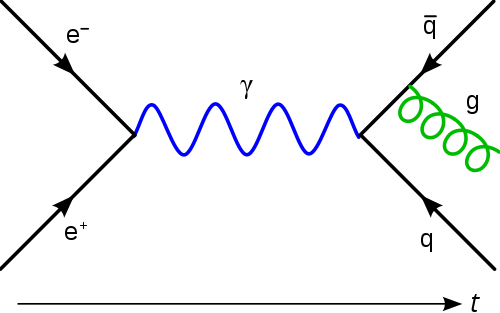
In this Feynman diagram, an electron (e–) and a positron (e+) annihilate, producing a photon (γ, represented by the blue sine wave) that becomes a quark–antiquark pair (quark q, antiquark q̄), after which the antiquark radiates a gluon (g, represented by the green helix). The idea of a gauge theory evolved from the work of Hermann Weyl. One can find in an interesting discussion of the history of gauge symmetry and the discovery of Yang–Mills theory, also known as “non-abelian gauge theory.” At the classical level one replaces the gauge group U(1) of electromagnetism by a compact gauge group G. The most important Quantum Field Theories (QFTs) for describing elementary particle physics are gauge theories. The classical example of a gauge theory is Maxwell’s theory of electromagnetism. For electromagnetism the gauge symmetry group is the abelian group U(1). If A denotes the U(1) gauge connection, locally a one-form on space-time, then the curvature or electromagnetic field tensor is the two-form F = dA, and Maxwell’s equations in the absence of charges and currents read 0 = dF = d * F. Here * denotes the Hodge duality operator; indeed, Hodge introduced his celebrated theory of harmonic forms as a generalization of the solutions to Maxwell’s equations. Maxwell’s equations describe large-scale electric and magnetic fields and also—as Maxwell discovered—the propagation of light waves, at a characteristic velocity, the speed of light.
The definition of the curvature arising from the connection must be modified to F = dA + A ^ A, and Maxwell’s equations are replaced by the Yang–Mills equations, 0 = dAF = dA* F, where dA is the gauge-covariant extension of the exterior derivative. These classical equations can be derived as variational equations from the Yang– Mills Lagrangian
L = 1/4g2 ∫ Tr F ^ F,
where Tr denotes an invariant quadratic form on the Lie algebra of G. The Yang– Mills equations are nonlinear—in contrast to the Maxwell equations. Like the Einstein equations for the gravitational field, only a few exact solutions of the classical equation are known. But the Yang–Mills equations have certain properties in common with the Maxwell equations: In particular they provide the classical description of massless waves that travel at the speed of light.
In mathematical terminology, electron phases form an Abelian group under addition, called the circle group or U(1). “Abelian” means that addition commutes, so that θ + φ = φ + θ. Group means that addition associates and has an identity element, namely “0”. Also, for every phase there exists an inverse such that the sum of a phase and its inverse is 0. Other examples of abelian groups are the integers under addition, 0, and negation, and the nonzero fractions under product, 1, and reciprocal.
Quick note

As a way of visualizing the choice of a gauge, consider whether it is possible to tell if a cylinder has been twisted. If the cylinder has no bumps, marks, or scratches on it, we cannot tell. We could, however, draw an arbitrary curve along the cylinder, defined by some function θ(x), where x measures distance along the axis of the cylinder. Once this arbitrary choice (the choice of gauge) has been made, it becomes possible to detect it if someone later twists the cylinder.
The non-abelian gauge theory of the strong force is called Quantum Chromodynamics (QCD). The use of QCD to describe the strong force was motivated by a whole series of experimental and theoretical discoveries made in the 1960s and 1970s, involving the symmetries and high-energy behavior of the strong interactions. But classical nonabelian gauge theory is very different from the observed world of strong interactions; for QCD to describe the strong force successfully, it must have at the quantum level the following three properties, each of which is dramatically different from the behavior of the classical theory:
- It must have a “mass gap;” namely there must be some constant Δ > 0 such that every excitation of the vacuum has energy at least Δ.
- It must have “quark confinement,” that is, even though the theory is described in terms of elementary fields, such as the quark fields, that transform non-trivially under SU(3), the physical particle states—such as the proton, neutron, and pion—are SU(3)-invariant.
- It must have “chiral symmetry breaking,” which means that the vacuum is potentially invariant (in the limit, that the quark-bare masses vanish) only under a certain subgroup of the full symmetry group that acts on the quark fields.
The first point is necessary to explain why the nuclear force is strong but short-ranged; the second is needed to explain why we never see individual quarks; and the third is needed to account for the “current algebra” theory of soft pions that was developed in the 1960s. Both experiment—since QCD has numerous successes in confrontation with experiment—and computer simulations, carried out since the late 1970s, have given strong encouragement that QCD does have the properties cited above. These properties can be seen, to some extent, in theoretical calculations carried out in a variety of highly oversimplified models (like strongly coupled lattice gauge theory). But they are not fully understood theoretically; there does not exist a convincing, whether or not mathematically complete, theoretical computation demonstrating any of the three properties in QCD, as opposed to a severely simplified truncation of it.
The Problem
To establish existence of four-dimensional quantum gauge theory with gauge group G, one should define a quantum field theory (in the above sense) with local quantum field operators in correspondence with the gauge-invariant local polynomials in the curvature F and its covariant derivatives, such as Tr FijFkl(x). Correlation functions of the quantum field operators should agree at short distances with the predictions of asymptotic freedom and perturbative renormalization theory, as described in textbooks. Those predictions include among other things the existence of a stress tensor and an operator product expansion, having prescribed local singularities predicted by asymptotic freedom. Since the vacuum vector Ω is Poincar´e invariant, it is an eigenstate with zero energy, namely HΩ = 0. The positive energy axiom asserts that in any quantum field theory, the spectrum of H is supported in the region [0,∞). A quantum field theory has a mass gap Δ if H has no spectrum in the interval (0, Δ) for some Δ > 0. The supremum of such Δ is the mass m, and we require m < ∞.Yang–Mills Existence and Mass Gap. Prove that for any compact simple gauge group G, a non-trivial quantum Yang–Mills theory exists on R4 and has a mass gap Δ > 0.
Mathematical Perspective
Wightman and others have questioned for approximately fifty years whether mathematically well-defined examples of relativistic, nonlinear quantum field theories exist. We now have a partial answer: Extensive results on the existence and physical properties of nonlinear QFTs have been proved through the emergence of the body of work known as “constructive quantum field theory” (CQFT). The answers are partial, for in most of these field theories one replaces the Minkowski space-time M4 by a lower-dimensional space-time M2 or M3, or by a compact approximation such as a torus. (Equivalently in the Euclidean formulation one replaces Euclidean space-time R4 by R2 or R3.) Some results are known for Yang Mills theory on a 4-torus T4 approximating R4, and, while the construction is not complete, there is ample indication that known methods could be extended to construct Yang–Mills theory on T4. In fact, at present we do not know any non-trivial relativistic field theory that satisfies the Wightman (or any other reasonable) axioms in four dimensions. So even having a detailed mathematical construction of Yang–Mills theory on a compact space would represent a major breakthrough. Yet, even if this were accomplished, no present ideas point the direction to establish the existence of a mass gap that is uniform in the volume. Nor do present methods suggest how to obtain the existence of the infinite volume limit T4 ➜ R4.
Processing…Success! You're on the list.Whoops! There was an error and we couldn't process your subscription. Please reload the page and try again.