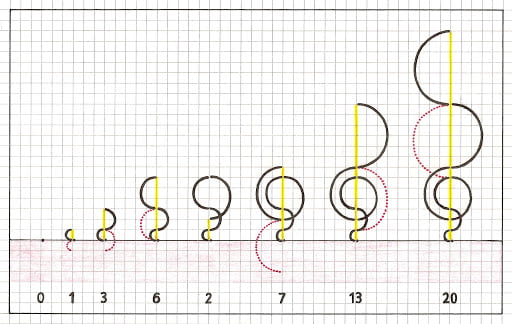
The Recamán Sequence

August 8, 2020 - By Rajarshi Dey

Recamán’s sequence was named after its inventor, Colombian mathematician Bernardo Recamán Santos, by Neil Sloane, creator of the On-Line Encyclopedia of Integer Sequences (OEIS). It is a well known sequence defined by a recurrence relation. In computer science they are often defined by recursion.

The Recamán Sequence is defined by-

{\displaystyle a_{n}={\begin{cases}0&&{\text{if }}n=0\\a_{n-1}-n&&{\text{if }}a_{n-1}-n>0{\text{ and is not already in the sequence}}\\a_{n-1}+n&&{\text{otherwise}}\end{cases}}}

According to this sequence first few elements are- 0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, 77, 39, 78, 38, 79, 37, 80, 36, 81, 35, 82, 34, 83, 33, 84, 32, 85, 31, 86, 30, 87, 29, 88, 28, 89, 27, 90, 26, 91, 157, 224…

The sequence satisfies $a_{n}\geq 0$ $|a_{n}-a_{n-1}|=n$ This is not a permutation of the integers: the first repeated term is $42=a_{24}=a_{20}$ Another one is $43=a_{18}=a_{26}$ Neil Sloane has conjectured that every number eventually appears, but it has not been proved. Even though 10¹⁵ terms have been calculated (in 2018), the number 852,655 has not appeared on the list.

MATLAB CODE FOR Recamán Sequence

n=65; % Number of Terms in the Sequence
A = zeros(1,n);
A(1) = 0;
for ii = 1:n-1 % Algorithm to create the sequence
b = A(ii)-ii;
A(ii+1) = b + 2*ii;
if b > 0 && ~any(A == b)
A(ii + 1) = b;
end
end
hold on;
axis equal;
for i = 2:1:n % Plotting the Graphs
y = 0; x = (A(i)+A(i-1))/2; r = (A(i)-A(i-1))/2;
th = 0:pi/50:pi;
if A(i)>A(i-1)
xunit = r * cos(th) + x;
yunit = r * sin(th) + y;
end
if A(i)<A(i-1)
xunit = -r * cos(th) + x;
yunit = -r * sin(th) + y;
end
if mod(i,2) == 0
h = plot(xunit, -yunit,'k');
else
h = plot(xunit, yunit,'k');
end
end