Banach–Tarski Paradox
The Banach–Tarski paradox is a theorem in set-theoretic geometry, which states the following: Given a solid ball in 3‑dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball. Indeed, the reassembly process involves only moving the pieces around and rotating them without changing their shape. However, the pieces themselves are not “solids” in the usual sense, but infinite scatterings of points. The reconstruction can work with as few as five pieces.
Dissection and reassembly of a figure is an important concept in classical geometry. It was used extensively by the Greeks to derive theorems about area, including the well-known Pythagorean Theorem.


Any two polygons with the same area are congruent by dissection
Proof-
First, observe that congruence by dissection is an equivalence relation. To see transitivity, suppose that a polygon Q can be dissected along some set of cuts into pieces that can be rearranged to form P, and can also be dissected along another set of cuts into pieces that form R. Then by making both sets of cuts, we end up with a set of pieces that can be rearranged to form either P or R; composing these two procedures, we get that P and R are congruent by dissection. Now it is sufficient to show that every polygon is congruent by dissection to a square. To do this, dissect the polygon into triangles. Each of these triangles is easily dissected into a rectangle, and then into a square.
Lebesgue Measure

In order to formalize our notions of length, area, and volume, we want a definition of measure that assigns nonnegative reals (or ∞) to subsets of Rn, with the following properties.
An n-dimensional hypercube of side x has measure xn.
The measure of the union of finitely many disjoint figures Ai ⊆ Rn is the sum of their measures. (One could also ask for countable additivity instead of just finite additivity, but we will not consider such cases here.)
One such definition is the Lebesgue measure (which is in fact countably additive). However, there is a serious caveat: it will turn out that it is not defined for all sets. The construction of the Lebesgue measure is somewhat technical; one definition is as follows.
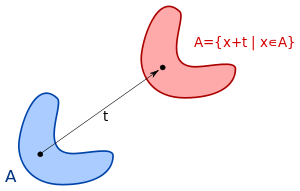
For any subset B ⊆ R2, define λ∗(B) to be the infimum of all k ∈ [0,∞] such that B can covered by a countable set of hypercubes with total measure k. Then we say that A ⊆ R2 is Lebesgue measurable if λ∗(B) = λ∗(A ∩ B) + λ∗(B r A) for all B ⊆ Rn; if so, its Lebesgue measure is defined to be λ(A) = λ∗(A).
Construction of the Paradox
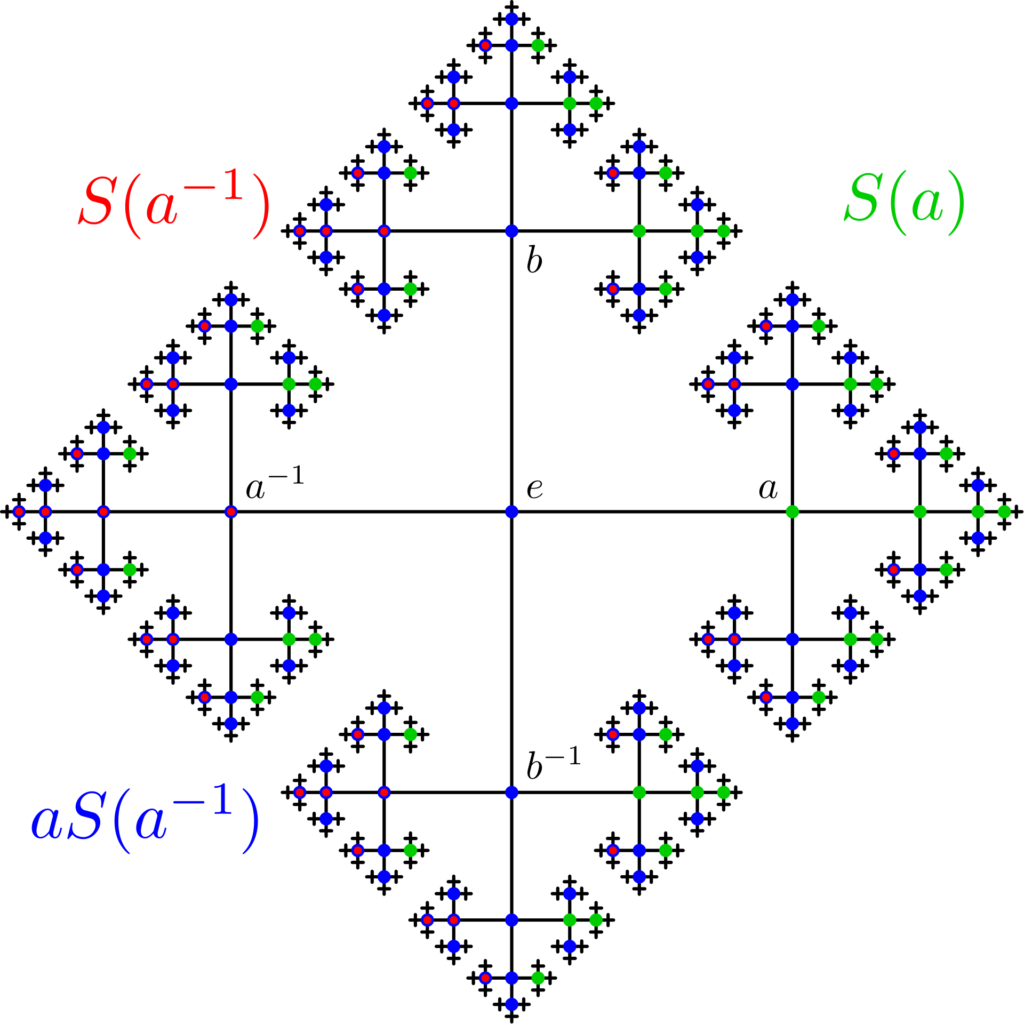

Our goal is to show that the unit ball B3 is equi-decomposable with two unit balls under the isometry group of R3 . We will show how to do this for a spherical shell S 2 . Then we can view most of the ball as a collection of spherical shells of radii 0 < r < 1, and apply the same transformations to each shell. This lets us take care of every point except the center. Our first task, then, is to show how to remove the center.
Lemma- B3 is equi-decomposable with B3 r {0}, where 0 is the ball’s center.
Proof. Consider a small circle that passes through 0 and is contained entirely in B3. Let ρ be a 1-radian rotation of this circle. Then the points 0, ρ0, ρ20, ρ30, . . . are distinct, and if we apply ρ to just this set of points, we get the same set except with 0 missing. This yields a two-piece equi-decomposition of B3 with B3 r {0}: one piece is {0, ρ0, ρ20, ρ30, . . . } going to {ρ0, ρ20, ρ30, . . . } under the rotation ρ, and the other d piece is the rest of the ball going to itself.
Theorem (Banach-Tarski Paradox) The unit ball B3 is equi-decomposable with two copies of itself.
Proof. We see that S 2 is equi-decomposable with two copies of itself. Scaling this construction about the center allows us to do this for the spherical shells of radius r, for any 0 < r < 1, with the same rotations. If we do this for all these shells simultaneously, we get an equi-decomposition of B3 r{0} with two copies of itself. Finally, we see that B3 is equi-decomposable with two copies of itself.
With some care, it can be shown that this equi-decomposition can be carried out using just five pieces. Somehow, making some cuts with the Axiom of Choice has allowed us to completely subvert the intuitive properties of volume. As promised, it is now a simple extension to equi-decompose any two bounded sets with nonempty interior.
At first glance, the Banach-Tarski Paradox appears to be an actual contradiction with measure theory, for if we measure all the pieces used in the construction, they must add up both to the volume of the ball and to twice the volume of the ball, and these are different positive real numbers. The resolution of this paradox is that the pieces must not be Lebesgue measurable—or more generally, any function that satisfies the properties of measure listed above cannot be defined on these piece.