Fuzzy logic is an approach to computing based on “degrees of truth” rather than the usual “true or false” (1 or 0) Boolean logic.
FUZZY SETS
A Fuzzy set is a class of objects with a continuum of grades of membership. Such a set is characterized by a membership (characteristic) function which assigns to each object a grade of membership ranging between zero and one. The notions of inclusions, unions, intersection, complement, relation and convexity are extended to such sets, and various properties of these notions in the context of various fuzzy sets are established.
A fuzzy set is a set containing elements that have a varying degree of membership in the set. Elements of a fuzzy set are mapped to a universe of membership values using function – theoretic form.
A notation convention for fuzzy sets, when the universe of discourse, X, is discrete and finite, is as follows for a fuzzy set A:
A = {(μ A (x1))/x1 + (μ A (x2))/x2 + ………..}
= Σ {(μ A (xi))/xi}
When the universe is continuous and infinite, the fuzzy set A is denoted by:
A = ∫ {(μ A (x))/x} (the ‘division sign’ is not a quotient but a delimiter).
- The numerator in each term is the membership value in set A associated with the element of the universe indicated in the denominator.
- The summation symbol is not for algebraic summation but rather a collection/aggregation.

FUZZY SET OPERATION
Define three fuzzy sets on the universe X. For a given element x of the universe, the following function – theoretic operations for the set-theoretic operations of union, intersection and complement are defined A, B and C on X :
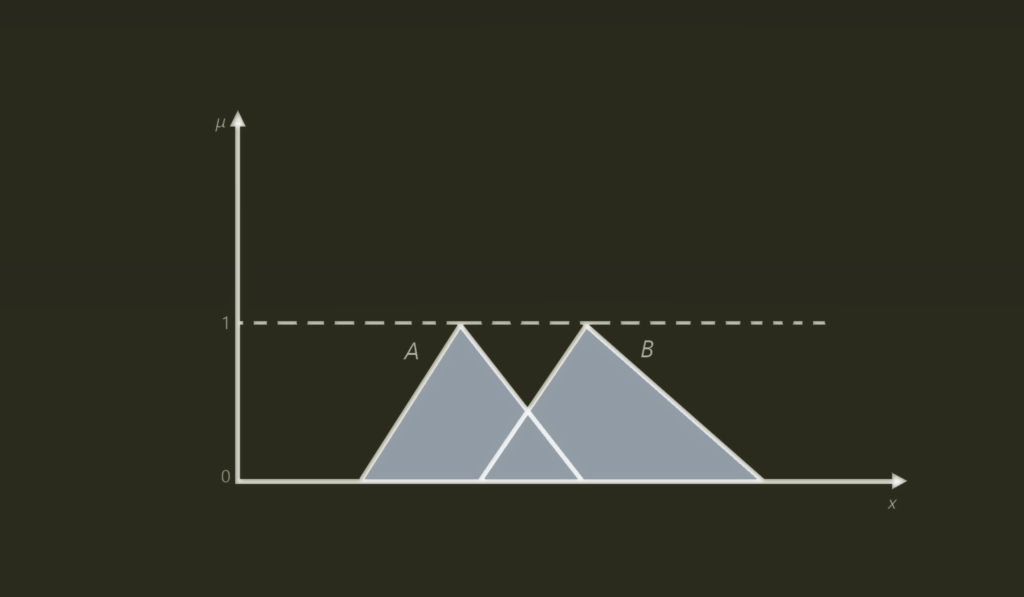
UNION
μ A∪B (x) = μ A (x) ∨ μ B (x)

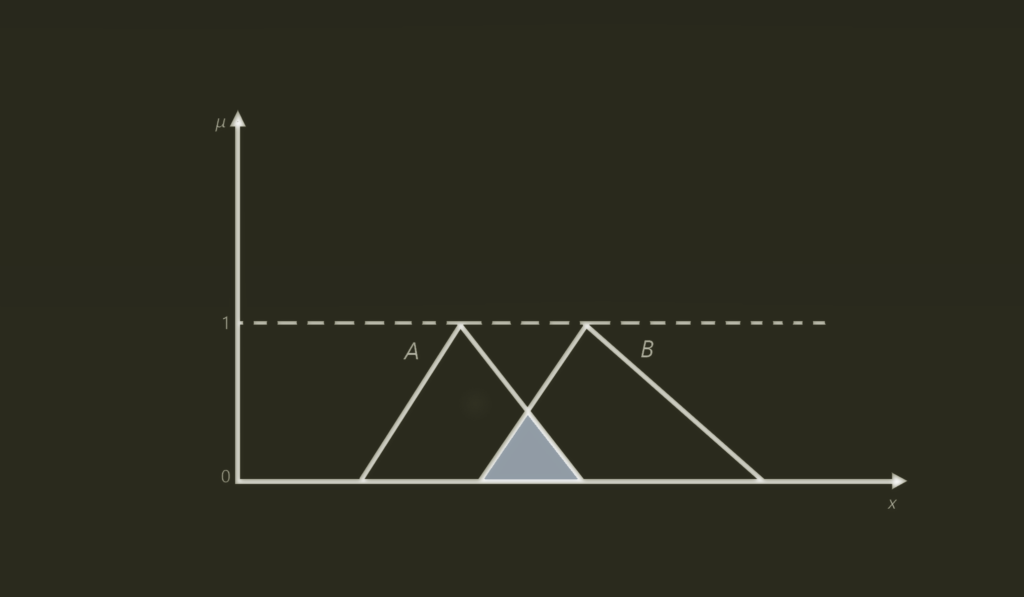

INTERSECTION
μ A∩B (x) = μ A (x) ∧ μ B (x)
COMPLEMENT
A ⊆ X → μ A (x) ≤ μ X (x)
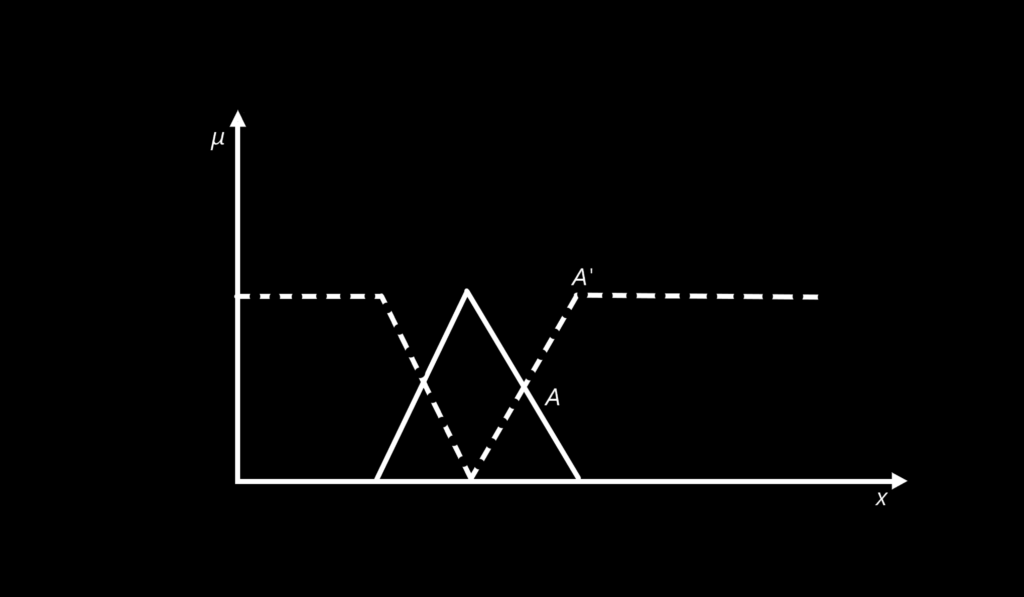

| LAW OF CONTRADICTION | LAW OF EXCLUDED MIDDLE |
|---|---|
| A ∩ A‘ = ϕ | A ∪ A‘ = X |
| OPERATION | CRISP RELATION | FUZZY RELATION |
|---|---|---|
| UNION | X A∪B (x, y) : X A∪B (x, y) = max [ X A (x, y) , X B (x, y) ] | μ A∪B (x, y) = max ( μ A (x, y) , μ B (x, y)) |
| INTERSECTION | X A∩B (x, y) : X A∩B (x, y) = min [ X A (x, y) , X B (x, y) ] | μ A∩B (x, y) = min ( μ A (x, y) , μ B (x, y)) |
| COMPLEMENT | X A’ (x, y) : X A’ (x, y) = 1 – X A (x, y) | μ A‘ (x, y) = 1 – μ A (x, y) |
| CONTAINMENT | X A (x, y) : X A (x, y) ≤ X B (x, y) | A ⊆ B → μ A (x) ≤ μ B (x) |
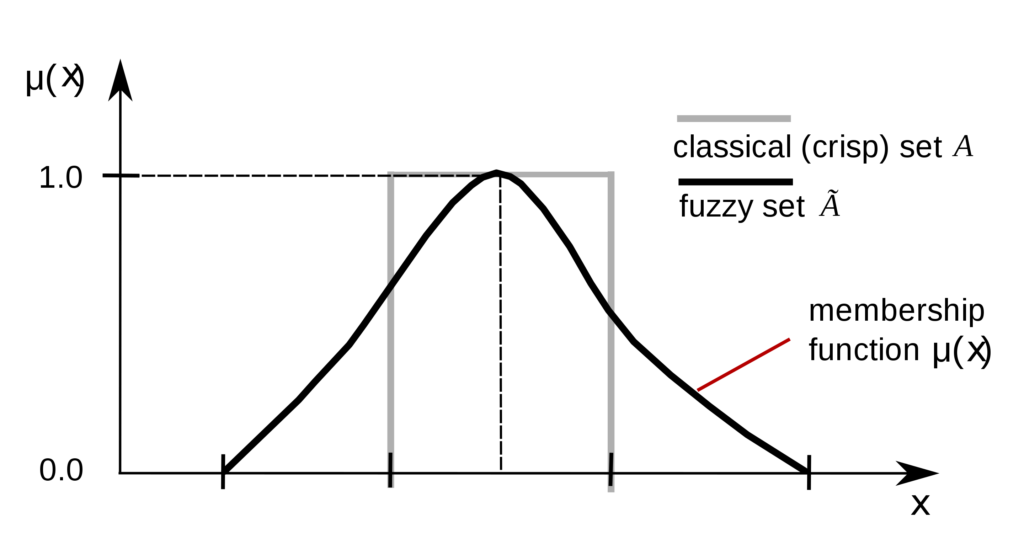

MEMBERSHIP FUNCTION
Membership functions represent fuzzy subsets of X. The membership function which represents a fuzzy set A is usually denoted by μ A. For an element x of X, the value μ A (x) is called the membership degree of x in the fuzzy set A The membership degree μ A (x) quantifies the grade of membership of the element x to the fuzzy set A. The value 0 means that x is not a member of the fuzzy set; the value 1 means that x is fully a member of the fuzzy set. The values between 0 and 1 characterize fuzzy members, which belong to the fuzzy set only partially.
Since all information contained in a fuzzy set is described by its membership function, it is useful to develop a lexicon of terms to describe various special features of this function. For purposes of simplicity, the functions shown in the following figures will all be continuous, but the terms apply equally for both discrete and continuous fuzzy sets.
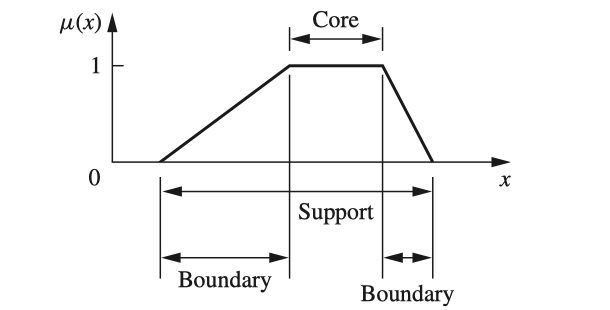

- The core of a membership function for some fuzzy set A is defined as that region of the universe that is characterized by complete and full membership in the set A. That is, the core comprises those elements x of the universe such that μA(x) = 1.
- The support of a membership function for some fuzzy set A is defined as that region of the universe that is characterized by nonzero membership in the set A. That is, the support comprises those elements x of the universe such that μA(x) > 0.
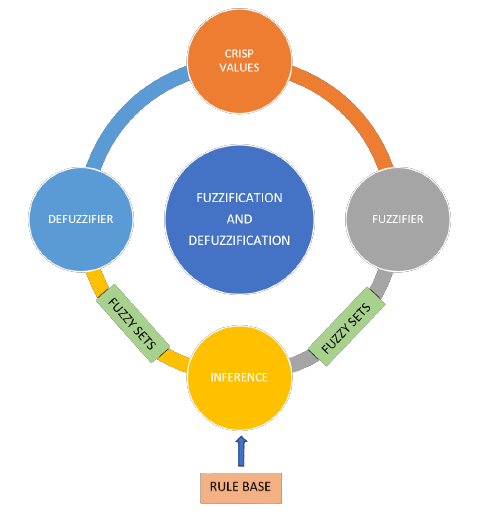
Implementing a Linguistic
Control strategy sensors for the crane head position Distance and the angle of the container sway Angle are employed to automate the control of this crane. Using these inputs to describe the current condition of the crane, for example,
IF Distance = medium AND Angle = neg_small THEN Power = pos_high
The figure below shows the complete structure of a fuzzy logic controller:
//CODE SAMPLE
//Fuzzy function to produce optimized power
public double fuzzy()
{
//Fuzzification of variables, distance and angle
if((angle<-60)&&(angle>=-90))
neg_small=0;
else if((angle<-10)&&(angle>=-60))
neg_small=(0.02*angle+1.2);
else if((angle<0)&&(angle>=-10))
neg_small=(-0.1*angle);
else if((angle<=90)&&(angle>=0))
neg_small=0;
if((angle<-60)&&(angle>=-90))
neg_big=1;
else if((angle>=-60)&&(angle<-10))
neg_big=(-0.02*angle-0.2);
else if((angle>=-10)&&(angle<=90))
neg_big=0;
if((distance<5)&&(distance>=-10))
medium=0;
else if((distance<10)&&(distance>=5))
medium=(0.2*distance-1);
else if((distance<22)&&(distance>=10))
medium=((-1/12)*distance+(11/6));
else if((distance<=30)&&(distance>=22))
medium=0;
if((distance<10)&&(distance>=-10))
far=0;
else if((distance<22)&&(distance>=10))
far=((1/12)*distance-(5/6));
else if((distance<=30)&&(distance>=22))
far=1;
//... other if_ then_else clauses for other terms of distance and angle to be
// continued .
//Defuzzification of variable, power
return
System.Math.Round(System.Math.Max(System.Math.Min(pos_small,zerodis),
System.Math.Min(pos_small,close))*neg_medium_pow+System.Math.Max(
System.Math.Min(zero,zerodis),System.Math.Min(zero,close))*zero_pow+System.Math.Max(
System.Math.Max(System.Math.Min(neg_small,close),System.Math.Min(neg_big,medium)),
System.Math.Min(zero,far))*pos_medium_pow+System.Math.Max(System.Math.Min(neg_small,
medium),System.Math.Min(neg_small,far))*pos_high_pow,2);
}



