Poincaré Conjecture
If we stretch a rubber band around the surface of an apple, then we can shrink it down to a point by moving it slowly, without tearing it and without allowing it to leave the surface. On the other hand, if we imagine that the same rubber band has somehow been stretched in the appropriate direction around a doughnut, then there is no way of shrinking it to a point without breaking either the rubber band or the doughnut. We say the surface of the apple is “simply connected,” but that the surface of the doughnut is not. Poincaré, almost a hundred years ago, knew that a two dimensional sphere is essentially characterized by this property of simple connectivity, and asked the corresponding question for the three dimensional sphere.
Clay Mathematics Institute
PROBLEM STATEMENT
If a compact three-dimensional manifold M3 has the property that every simple closed curve within the manifold can be deformed continuously to a point, does it follow that M3 is homeomorphic to the sphere S3?
Henri Poincare’ commented, with considerable foresight, “Mais cette question nous entraˆınerait trop loin”. Since then, the hypothesis that every simply connected closed 3-manifold is homeomorphic to the 3-sphere has been known as the Poincare’ Conjecture. It has inspired topologists ever since, and attempts to prove it have led to many advances in our understanding of the topology of manifolds. From the first, the apparently simple nature of this statement has led mathematicians to overreach. Four years earlier, in 1900, Poincare’ himself had been the first to err, stating a false theorem that can be phrased as follows.
HIGHER DIMENSIONS
The fundamental group plays an important role in all dimensions even when it is trivial, and relations between generators of the fundamental group correspond to two-dimensional disks, mapped into the manifold. In dimension 5 or greater, such disks can be put into general position so that they are disjoint from each other, with no self-intersections, but in dimension 3 or 4 it may not be possible to avoid intersections, leading to serious difficulties. Stephen Smale announced a proof of the Poincare’ Conjecture in high dimensions in 1960. He was quickly followed by John Stallings, who used a completely different method, and by Andrew Wallace, who had been working along lines quite similar to those of Smale.
The Ricci Flow


Let M be an n-dimensional complete Riemannian manifold with the Riemannian metric gij . The Levi-Civita connection is given by the Christoffel symbols


where gij is the inverse of gij . The summation convention of summing over repeated indices is used here and throughout the book. The Riemannian curvature tensor is given by


We lower the index to the third position, so that
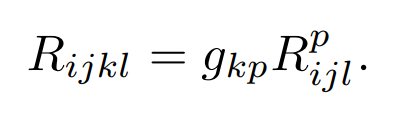

The curvature tensor Rijkl is anti-symmetric in the pairs i, j and k, l and symmetric in their interchange:


Also the first Bianchi identity holds
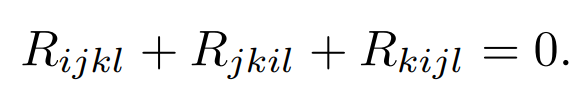

The Ricci tensor is the contraction
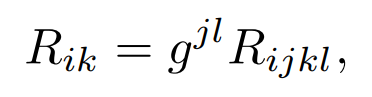

and the scalar curvature is
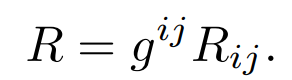

We denote the covariant derivative of a vector field v = vj (∂/∂xj)by
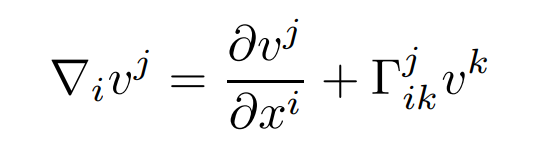

and of a 1-form by
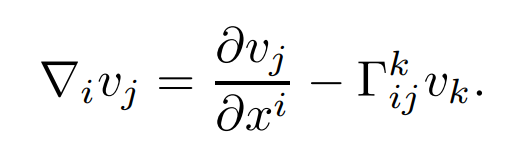

These definitions extend uniquely to tensors so as to preserve the product rule and contractions. For the exchange of two covariant derivatives, we have
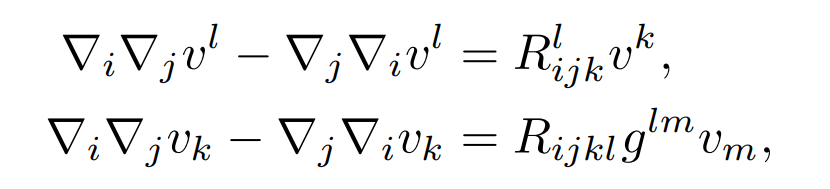

and similar formulas for more complicated tensors. The second Bianchi identity is given by
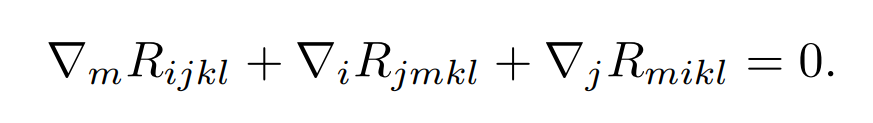

For any tensor T = Tijk we define its length by
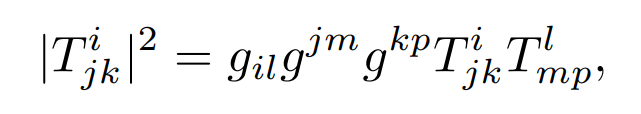

and we define its Laplacian by


the trace of the second iterated covariant derivatives. Similar definitions hold for more general tensors.
The Ricci flow of Hamilton is the evolution equation


for a family of Riemannian metrics gij (t) on M. It is a nonlinear system of second order partial differential equations on metrics.
In August 2006, Grigory Perelman was offered the Fields Medal for “his contributions to geometry and his revolutionary insights into the analytical and geometric structure of the Ricci flow”, but he declined the award, stating: “I’m not interested in money or fame; I don’t want to be on display like an animal in a zoo.” On 22 December 2006, the scientific journal Science recognized Perelman’s proof of the Poincaré conjecture as the scientific “Breakthrough of the Year”, the first such recognition in the area of mathematics.