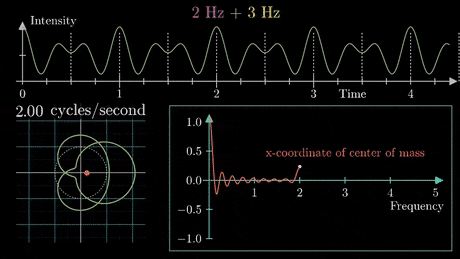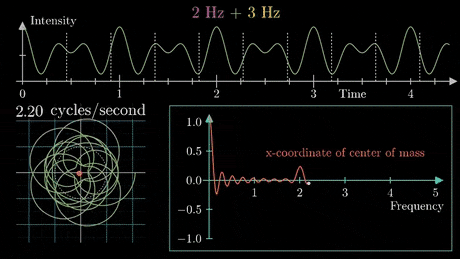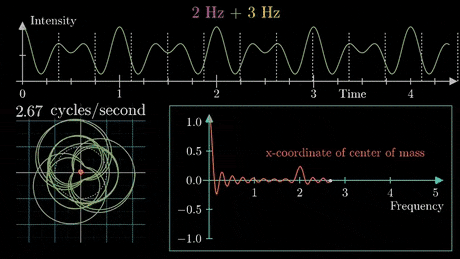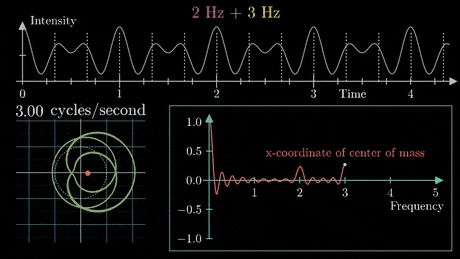
FOURIER SERIES FOR PERIODIC FUNCTIONS
Previously we have studied the derivation of Fourier Series from the equation of Heat Diffusion. Now the derivation would not stop a result this beautiful to spread fields of science like Engineering, Physics and Applied Mathematics. These infinite series are defined to represent general periodic functions, mainly the trigonometric functions.
Fourier Series is way more universal than other infinite series like the Taylor Series as many discontinuous periodic functions which have applications that can only be developed by Fourier Series.
Lets hover a little over some basic stuff.
Periodic Functions- A function f(x) is called a periodic function if it is defined for real x, and if there is a positive number p, such that:
f(x + p) = f(x), for all x.
Smallest positive period is called fundamental period.
Orthogonality Of Trigonometric Functions
- Orthogonality relations on the full period [−p, p]:
Let m and n be positive integers. Then,
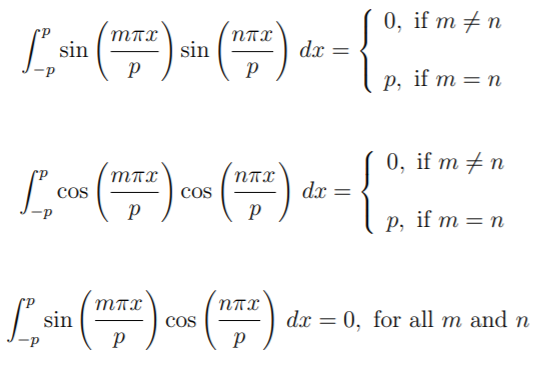

- Orthogonality relations on the half period [0, p]:
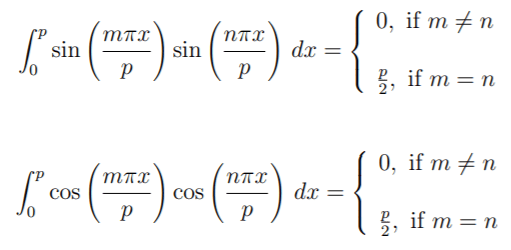

Dirichlet Conditions
In mathematics, the Dirichlet conditions are sufficient conditions for a real-valued, periodic function f to be equal to the sum of its Fourier series at each point where f is continuous. Moreover, the behavior of the Fourier series at points of discontinuity is determined as well (it is the midpoint of the values of the discontinuity). These conditions are named after Peter Gustav Lejeune Dirichlet.
The conditions are:
- f must be absolutely integrable over a period.
- f must be of bounded variation in any given bounded interval.
- f must have a finite number of discontinuities in any given bounded interval, and the discontinuities cannot be infinite.
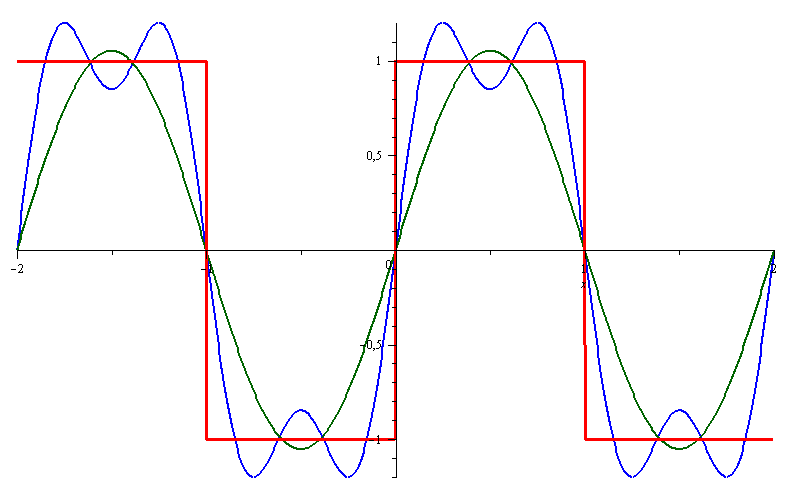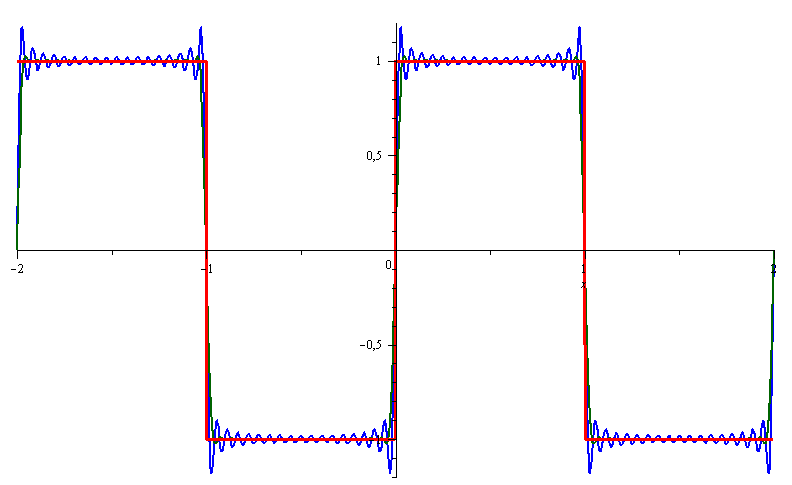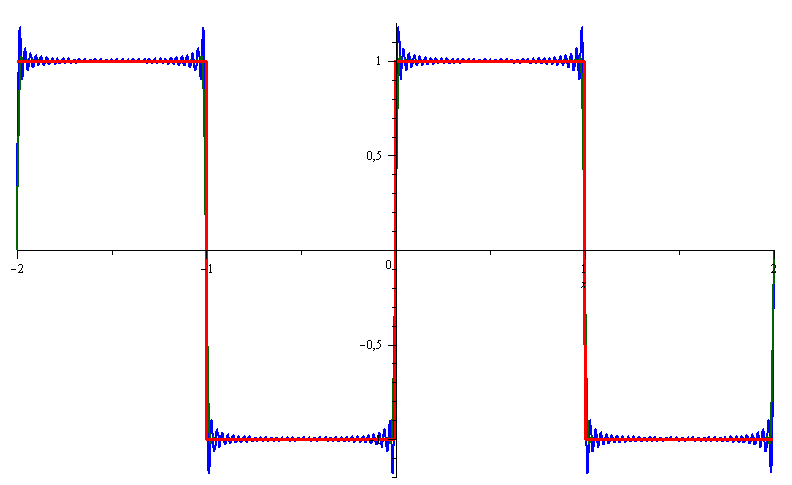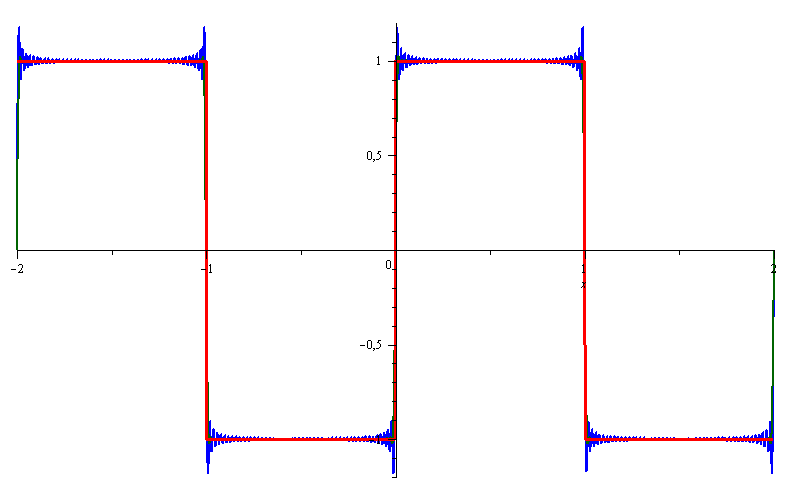

The General Fourier Series Representation
If we proceed with
a bar of length 2L stretching from −L to L and we assume that the temperature at its ends satisfy the boundary conditions,
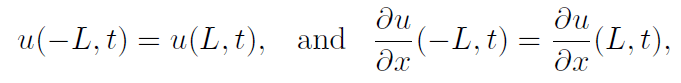

then one can show that the assumption of separation of variables, will
lead to the trial form
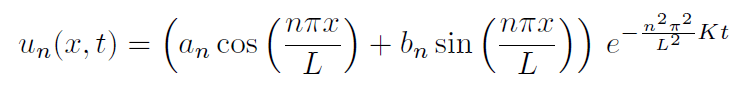

from which we obtain the general representation of u as,
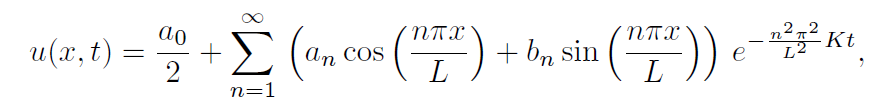

valid for all x, t under consideration. In this case, the initial configuration of
the rod given by u(x, 0) = f(x) will force the representation of f in the more general form,
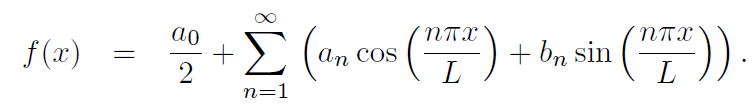

Fourier series representation of the function f on the interval [−L,L] having the Fourier coefficients given by an and bn. The an will be called the Fourier cosine coefficients while the bn will be called the Fourier sine coefficients. We’ll give the main idea on how to find the value of these Fourier coefficients . . .
If f(x) is defined on [−L,L] and f has the Fourier series representation given
by,
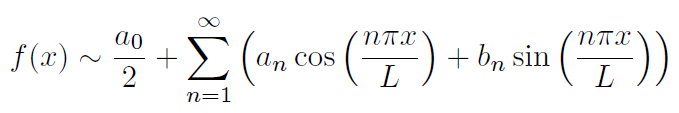

then the Fourier coefficients are all given by,
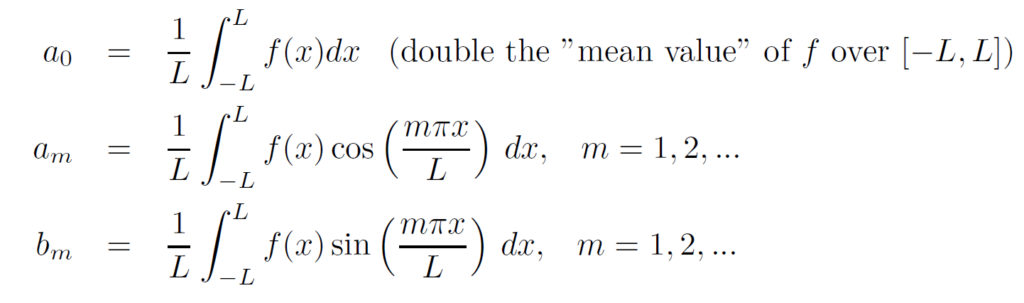

Even and Odd Functions
Before we proceed to an actual calculation of these quantities let’s look at some special classes of functions defined on a symmetric interval [−L,L].
We say that a function f is an even function on [−L,L] if for any symbols ±x in the domain of f we have, f(−x) = f(x).
Similarly, we say that a function f is an odd function on [−L,L] if for any symbols ±x in the domain of f we have, f(−x) = −f(x).
Geometrically an even function is a function f whose graph is symmetric with respect to the y-axis, while an odd function is a function f whose graph is symmetric with respect to the origin, O, (we call this a central reflection).
If f is an even function on the interval [−L,L] then its Fourier series must be a pure cosine series in the sense that,
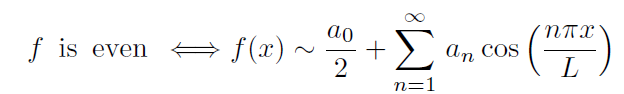

The reason for this is that since f is even and sin(nπx/L) is odd, then their product must be odd and so we see that,
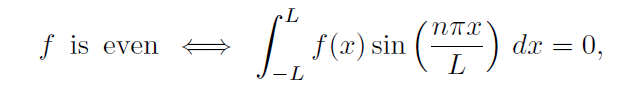

for n = 1, 2, . . . or equivalently, bn = 0 for each n = 1, 2, . . .
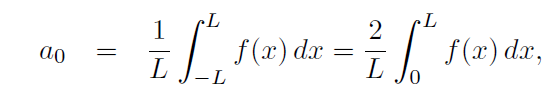

and since f is even,
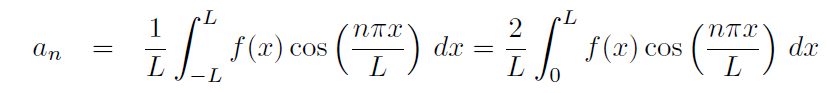

If f is an odd function on the interval [−L,L] then its Fourier series must be a pure sine series in the sense that,
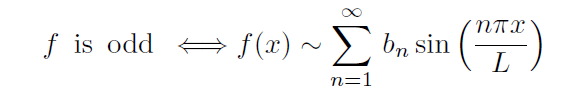

The reason for this is that since f is odd and cos(nπx/L) is even, then their product must be odd and so we see that,
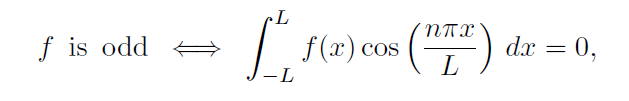

for n = 1, 2, . . . or equivalently, an = 0 for each n = 1, 2, . . .
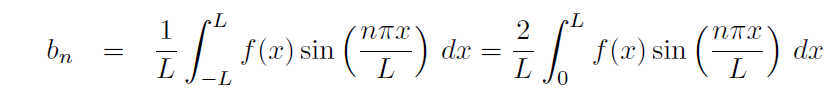

Conversely, it is also true that if f(x) has a representation as a pure sine series on [−L,L] then f must be an odd function on that interval.
Parseval’s Equality
If the function f satisfies the three conditions of the Dirichlet Test for convergence, then its Fourier coefficients have the property that,
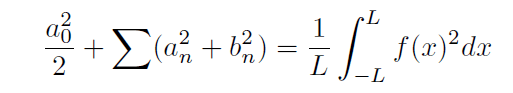

In general there always holds Bessel’s Inequality, that is,
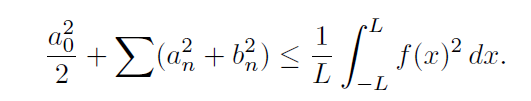

This result is valid for any function that is piece-wise continuous on (−L,L).
COURTESIES TO WIKIPEDIA AND IMAGE COURTESY TO 3 BLUE 1 BROWN.