In mathematics, a surface is a geometrical shape that resembles a deformed plane. The most familiar examples arise as boundaries of solid objects in ordinary three-dimensional Euclidean space R3, such as spheres. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not. A surface is a two-dimensional space; this means that a moving point on a surface may move in two directions (it has two degrees of freedom).
Historically, surfaces were initially defined as subspaces of Euclidean spaces. Often, these surfaces were defined as the locus of zeros of certain functions, usually polynomial functions. Such a definition considered the surface as part of a larger (Euclidean) space, and was termed extrinsic.


Definition. A parametrized continuous surface in R3 is a continuous map σ: U → R3, where U ⊂ R2 is an open, non-empty set.
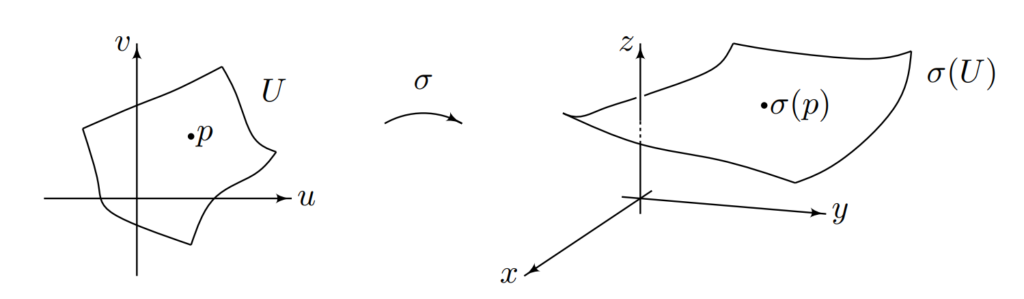

It will often be convenient to consider the pair (u, v) ∈ U as a set of coordinates of the point σ(u, v) in the image S = σ(U). However, since σ is not assumed to be injective, the same point in S may have several pairs of coordinates. We call a parametrized continuous surface smooth if the map σ: U → R3 is smooth, that is, if the components σi, where i = 1, 2, 3, of σ(u, v) = (σ1(u, v), σ2(u, v), σ3(u, v)) have continuous partial derivatives with respect to u and v, up to all orders. We adopt the convention that a parametrized surface is smooth, unless otherwise mentioned.
Example. Sphere. Let σ(u, v) = (cos u cos v, cos u sin v, sin u) where (u, v) ∈ R2. This is a standard parametrization of the unit sphere S2 = {(x, y, z) ∈ R3|x2 + y2 + z2 = 1}. The parameters u and v are called latitude and longitude, and together they are called spherical coordinates.
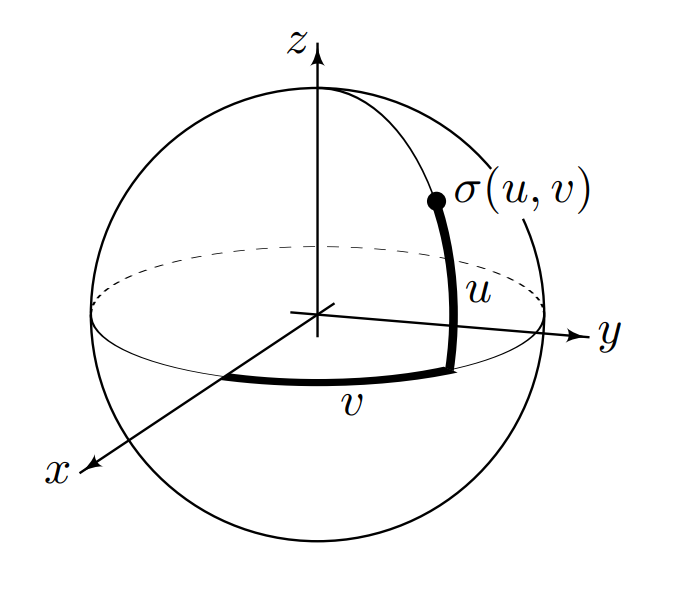

This parametrization covers the total sphere, but it is not injective. On the other hand, if we request, for example, that u ∈]−π/2,π/2[ and v ∈]−π, π[ then σ is injective, but it is not surjective, since a half-circle on the ‘back’ of the sphere will be outside the image of σ.
Level sets
Very often a plane curve is described, not by means of a parametrization, but by an equation. For example, a line is represented by an equation of the form ax+by = c with a, b, c ∈ R and (a, b) not equal to (0, 0), and a circle is represented by an equation of the form (x − x0)2 + (y − y0)2 = r2 with r > 0. Similarly a surface can be described by an equation. For example, a plane in R3 is the set of solutions to an equation ax + by + cz = d, where (a, b, c) not equal to (0, 0, 0), and a sphere is represented by (x−x0)2 + (y −y0)2 + (z −z0)2 = r2.
SURFACE GRADIENT
The gradient of a function f(x, y) is defined as ∇f(x, y) = {fx(x, y), fy(x, y)}. For functions of three dimensions, we define ∇f(x, y, z) = {fx(x, y, z), fy(x, y, z), fz(x, y, z)}.
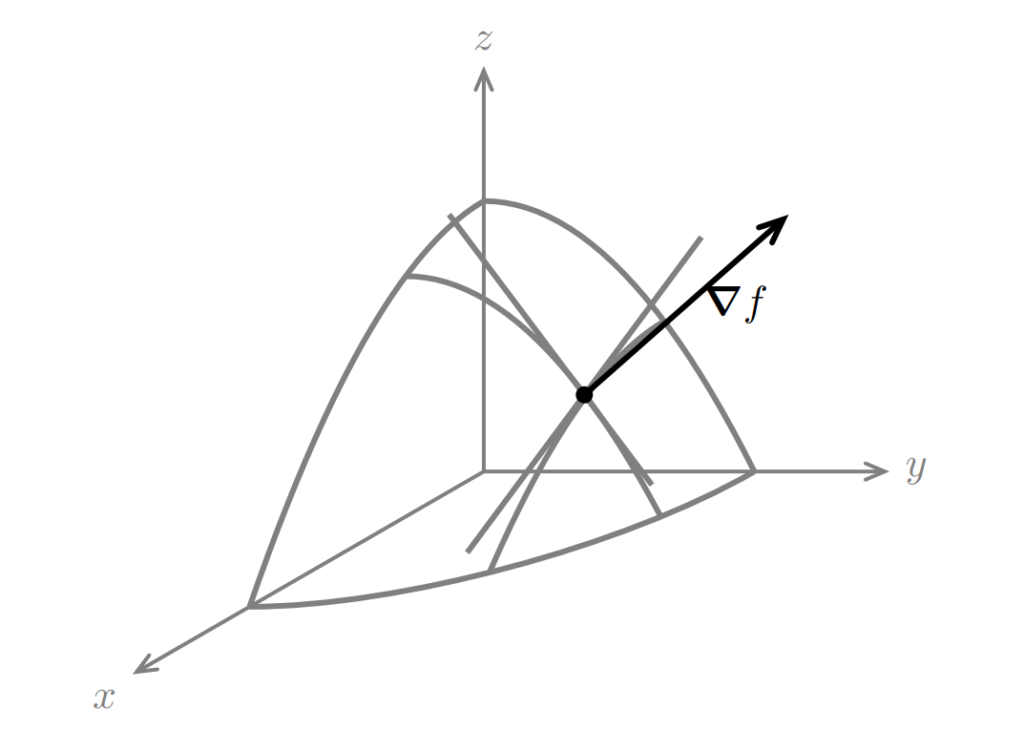
Gradients are orthogonal to level curves and level surfaces.
Let w = f(x, y, z) be a function of 3 variables. We will show that at any point
P = (x0, y0, z0) on the level surface f(x, y, z) = c (so f(x0, y0, z0) = c) the gradient ∇f|P is perpendicular to the surface. By this we mean it is perpendicular to the tangent to any curve that lies on the surface and
goes through P. This follows easily from the chain rule: Let
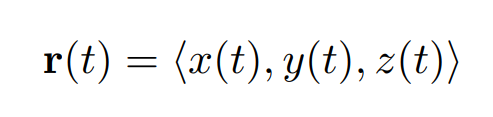

be a curve on the level surface with r(t0) = {x0, y0, z0}. We let g(t) = f(x(t), y(t), z(t)). Since the curve is on the level surface we have g(t) = f(x(t), y(t), z(t)) = c. Differentiating this equation with respect to t gives
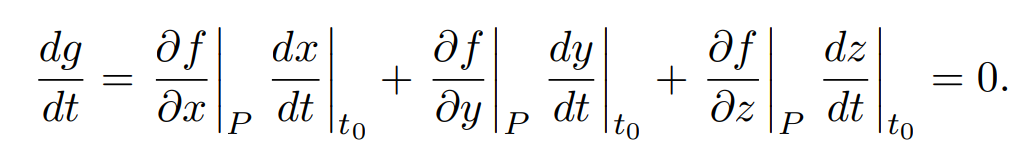

In vector form this is,
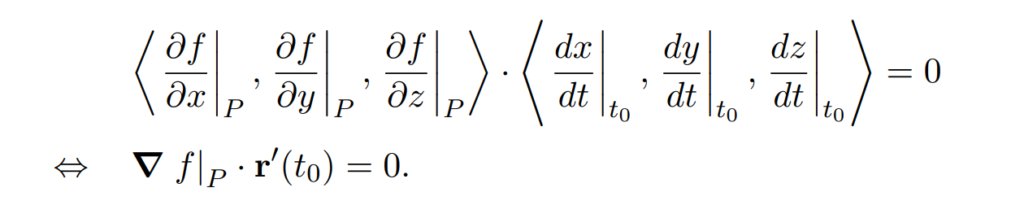

Since the dot product is 0, we have shown that the gradient is perpendicular to the tangent to any curve that lies on the level surface, which is exactly what we needed to show.

RIEMANN SURFACES
In mathematics, particularly in complex analysis, a Riemann surface is a one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together.
The main interest in Riemann surfaces is that holomorphic functions may be defined between them. Riemann surfaces are nowadays considered the natural setting for studying the global behavior of these functions, especially multi-valued functions such as the square root and other algebraic functions, or the logarithm.
Every Riemann surface is a two-dimensional real analytic manifold (i.e., a surface), but it contains more structure (specifically a complex structure) which is needed for the unambiguous definition of holomorphic functions. A two-dimensional real manifold can be turned into a Riemann surface (usually in several inequivalent ways) if and only if it is orientable and metrizable. So the sphere and torus admit complex structures, but the Möbius strip, Klein bottle and real projective plane do not.
MORE TO BE ADDED. STAY TUNED