

CHAOS THEORY
Chaos theory is a branch of mathematics focusing on the study of chaos states of dynamical systems whose apparently random states of disorder and irregularities are often governed by deterministic laws that are highly sensitive to initial conditions. When employing mathematical theorems, one should remain careful about whether their hypotheses are valid within the frame of the questions considered. Among such hypotheses in the domain of dynamics, a central one is the continuity of time and space (that an infinity of points exists between two points). This hypothesis, for example, may be invalid In the cognitive neurosciences of perception, where a finite time threshold often needs to be considered.
Birth of the chaos theory
Poincaré and phase space
With the work of Laplace, the past and the future of the solar system could be calculated and the precision of this calculation depended on the capacity to know the initial conditions of the system, a real challenge for “geometricians,” as alluded to by d’Holbach and Le Verrier. Henri Poincaré developed another point of view, as follows: in order to study the evolution of a physical system over time, one has to construct a model based on a choice of laws of physics and to list the necessary and sufficient parameters that characterize the system (differential equations are often in the model). One can define the state of the system at a given moment, and the set of these system states is named phase space.
The phenomenon of sensitivity to initial conditions was discovered by Poincaré in his study of the the n-body problem, then by Jacques Hadamard using a mathematical model named geodesic flow, on a surface with a nonpositive curvature, called Hadamard’s billards. A century after Laplace, Poincaré indicated that randomness and determinism become somewhat compatible because of the long-erm unpredictability.
A very small cause, which eludes us, determines a considerable effect that we cannot fail to see, and so we say that this effect Is due to chance. If we knew exactly the laws of nature and the state of the universe at the initial moment, we could accurately predict the state of the same universe at a subsequent moment. But even If the natural laws no longer held any secrets for us, we could still only know the state approximately. If this enables us to predict the succeeding state to the same approximation, that is all we require, and we say that the phenomenon has been predicted, that It Is governed by laws. But this is not always so, and small differences in the initial conditions may generate very large differences in the final phenomena. A small error in the former will lead to an enormous error In the latter. Prediction then becomes impossible, and we have a random phenomenon.
This was the birth of chaos theory.


Rebirth of chaos theory
Edward Lorenz, from the Massachusetts Institute of Technology (MIT) is the official discoverer of chaos theory. He first observed the phenomenon as early as 1961 and, as a matter of irony, he discovered by chance what would be called later the chaos theory, in 1963, while making calculations with uncontrolled approximations aiming at predicting the weather. The anecdote is of interest: making the same calculation rounding with 3-digit rather than 6-digit numbers did not provide the same solutions; indeed, in nonlinear systems, multiplications during iterative processes amplify differences in an exponential manner. By the way, this occurs when using computers, due to the limitation of these machines which truncate numbers, and therefore the accuracy of calculations.
Lorenz considered, as did many mathematicians of his time, that a small variation at the start of a calculation would Induce a small difference In the result, of the order of magnitude of the initial variation. This was obviously not the case, and all scientists are now familiar with this fact. In order to explain how important sensitivity the to initial conditions was, Philip Merilees, the meteorologist who organized the 1972 conference session where Lorenz presented his result, chose himself the title of Lorenz’s talk, a title that became famous: “Predictability: does the flap of a butterfly’s wing in Brazil set off a tornado in Texas?” This title has been cited and modified in many articles, as humorously reviewed by Nicolas Witkowski. Lorenz had rediscovered the chaotic behavior of a nonlinear system, that of the weather, but the term chaos theory was only later given to the phenomenon by the mathematician James A. Yorke, in 1975. Lorenz also gave a graphic description of his findings using his computer. The figure that appeared was his second discovery: the attractors.
The golden age of chaos theory
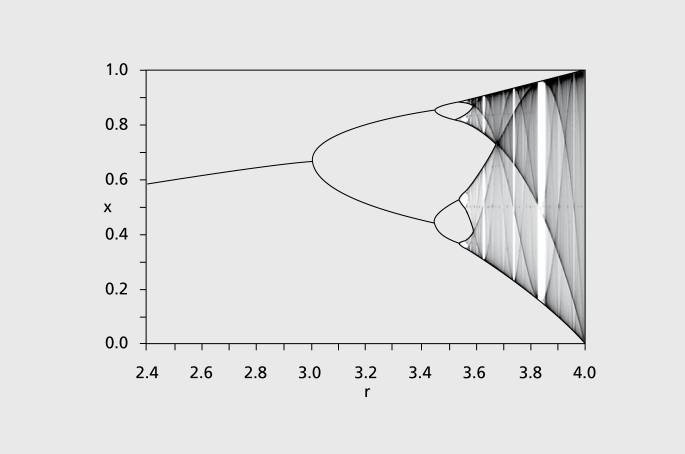
Felgenbaum and the logistic map
Mitchell Jay Feigenbaum proposed the scenario called period doubling to describe the transition between a regular dynamics and chaos. His proposal was based on the logistic map introduced by the biologist Robert M. May in 1976. While so far there have been no equations this text, I will make an exception to the rule of explaining physics without writing equations, and give here a rather simple example. The logistic map is a function of the segment [0,1] within itself defined by:
xn+1=rxn(1-xn)
where n = 0, 1, … describes the discrete time, the single dynamical variable, and 0≤r≤4 is a parameter. The dynamic of this function presents very different behaviors depending on the value of the parameter r:
For 0≤r≤3, the system has a fixed point attractor that becomes unstable when r=3.
Pour 3<r<3,57…, the function has a periodic orbit as attractor, of a period of 2n where n is an integer that tends towards infinity when r tends towards 3,57…
When r=3,57…, the function then has a Feigenbaum fractal attractor.
When over the value of r=4, the function goes out of the interval [0,1]

COURTESY- Christian Oestreicher, Department of Public Education, State of Geneva, Switzerland;* E-mail:hc.eg.ude@rehciertseo.naitsirhc










2 Comments
olivier denis
The initial state is a kaotic state of informational equilibrium
where the surplus of information at equilibrium is translated into order
therefore energy, light and sound ….
this occurs following The Meissner effect (or Meissner–Ochsenfeld effect)
https://entropicinformation.space/index.php/gravitationnal-analysis-tm
https://entropicinformation.space/index.php/gravitationnal-analysis-tm/the-meissner-effect-tm
Pingback: