FOURIER SERIES

A Fourier series is an expansion of a periodic function f(x) in terms of an infinite sum of sines and cosines. Fourier series make use of the orthogonality relationships of the sine and cosine functions. The computation and study of Fourier series is known as harmonic analysis and is extremely useful as a way to break up an arbitrary periodic function into a set of simple terms that can be plugged in, solved individually, and then recombined to obtain the solution to the original problem or an approximation to it to whatever accuracy is desired or practical.

Motivation and Derivation

Joseph-Louis Fourier, (1768-1830), a French engineer (and mathematician) discussed heat flow through a bar which gives rise to the so-called Heat Diffusion Problem, ∂2u/∂x2 =(1/K)(∂u/∂t) where u = u(x, t), K >0 is a constant depending on the thermal properties of the bar, u(0, t) = 0 = u(L, t), and u(x, 0) = f(x), where f is given at the outset. Think of f as being the initial state of the bar at time t = 0, and u(x, t) as being the temperature distribution along the bar at the point x in time t. The boundary conditions or conditions at the end-points are given in such a way that the bar’s “ends” are kept at a fixed temperature, say 0 degrees (whatever) and we can assume that most of the bar is at a temperature close to room temperature, for simplicity.

We apply the method of Separation of Variables first. Like Daniel Bernoulli
before him, Fourier assumed that the solution he was looking for had the form,
u(x, t) = f(x)g(t),
where we need to find these two functions f, g of one variable. Substituting this expression into the diffusion equation we find,

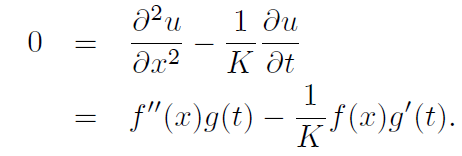
Dividing both sides by the product f(x)g(t) and separating out terms in x from terms in t we get,

Now this equality, is valid for any value of x where 0 < x < L and any value of t where t > 0. So we can let x = x0 where this number x0 is any fixed number in the interval [0, L]. Let,

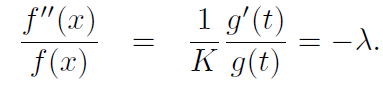
These equalities can be recast as two equations, namely,

Now the last equation is a constant coefficient first order linear differential equation and its general solution is given by,

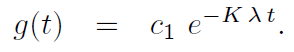
Arguing on physical grounds, the bar should reach a steady state as t → ∞
(i.e., the whole bar should ultimately be at a temperature of 0 as t→∞.) This
means that λ > 0, or else g(t) is exponentially large (since K > 0 too). As we know that λ > 0 then the general solution of the equation is,

where c2 and c3 are constants. Combining these expressions for f and g we get,

Fourier figured the solution and in order to get some values for the constants therein he must use the boundary conditions given at the ends of the rod, u(0, t) = 0 = u(L, t).

f(0)g(t) = 0 = f(L)g(t) for all t > 0. Since g(t) not equal to 0 we must have,
f(0) = 0 and f(L) = 0.

Since the zeros of the sine function occur at numbers of the form nπ where n is an integer, we see that √λL = nπ is necessary, that is,

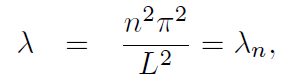
where n is an integer and we show the dependence of λ upon n by the symbol on the right, λn. So there are infinitely many possibilities for λ, as each one of these λ = λn (called eigenvalues) generates a solution,

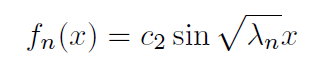
of the Sturm-Liouville equation

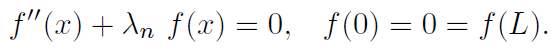
These special solutions fn(x) that satisfy both the equation and the boundary conditions are called eigen functions of the boundary value problem. Using these fn(x) we can construct u = un(x, t), where c3 = 0 and λ = λn,

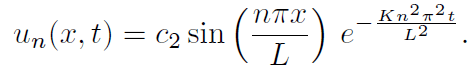
So, Fourier probably thought if one writes,

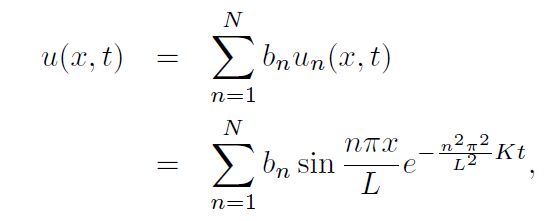
then this new function u(x, t) also satisfies along with the boundary conditions u(0, t) = u(L, t) = 0. But, once again, if f(x) is basically arbitrary it is not necessarily true that

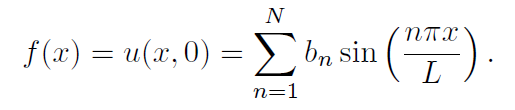
So, the great insight was the query, “What if f(x) can be represented as an
infinite series of such sine functions?”, that is, what if,

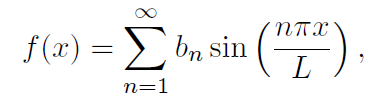
in the sense of convergence of the series on the right to f(x) for most x in [0, L]? It turned out that this could be done and the representation of f (where the constants bn depend on f) would eventually be an example of a Fourier Series! The solution of the original problem of heat conduction in a bar would then be solved analytically by the infinite series

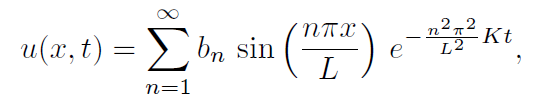
where the bn are called the Fourier coefficients of f on the interval [0, L].

Fourier actually gave a proof of the convergence of the series he developed (in his book on the theory of heat) yet it must be emphasized that Daniel Bernoulli before him solved the problem of the vibrating string by writing down the solution in terms of a “Fourier series” too!