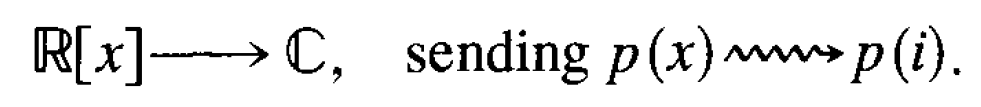The integers form our basic model for the concept of a ring. They are closed under addition, subtraction, and multiplication, but not under division.
Definition. A ring R is a set with two laws of composition + and x, called addition and multiplication, which satisfy these axioms:
(a) With the law of composition +, R is an abelian group, with identity denoted by O. This abelian group is denoted by R+.
(b) Multiplication is associative and has an identity denoted by 1.
(c) Distributive laws: For all a, b, c, E R, (a + b)c = ac + be and c(a + b) = ca + cb.
The terminology used is not completely standardized. Some people do not require the existence of a multiplicative identity in a ring. We will study commutative rings in most of this book, that is, rings satisfying the commutative law ab = ba for multiplication. So let us agree that the word ring will mean commutative ring with identity, unless we explicitly mention noncommutativity. The two distributive laws (c) are equivalent for commutative rings.
The ring Rnxn of all n x n matrices with real entries is an important example
of a ring which is not commutative.
Examples.
(a) Any field is a ring.
(b) The set R of continuous real-valued functions of a real variable x forms a ring, with addition and multiplication of functions: f + g = j(x) + g(x) and fg = j(x)g(x).
(c) The zero ring R = {O} consists of a single element O.
FORMAL CONSTRUCTION OF INTEGERS AND POLYNOMIALS
We learn that the ring axioms hold for the integers in elementary school. However, let us look again in order to see what is required in order to write down proofs of properties such as the associative and distributive laws. Complete proofs require a fair amount of writing, and we will only make a start here. It is customary to begin by defining addition and multiplication for positive integers. Negative numbers are introduced later. This means that several cases have to be treated as one goes along, which is boring, or else a clever notation has to be found to avoid such a case analysis. We will content ourselves with a description of the operations on positive integers. Positive integers are also called natural numbers.
The set N of natural numbers is characterized by these properties, called Peano’s axioms:
(a) The set N contains a particular element 1.
(b) Successor function: There is a map a: N~ N that sends every integer n ∈ N to another integer, called the next integer or successor. This map is injective, and for every n ∈ N, a (n) not equal to 1.
(c) Induction axiom: Suppose that a subset S of N has these properties:
(i) 1 ∈ S;
(ii) if n ∈ S then a (n) ∈ S.
Then S contains every natural number: S = N.
Proposition. There is a unique commutative ring structure on the set of
polynomials R [x] having these properties:
(a) Addition of polynomials is vector addition.
(b) Multiplication of monomials is given by the rule.
(c) The ring R is a subring of R[x], when the elements of R are identified with the constant polynomials.
HOMOMORPHISMS AND IDEALS
A homomorphism ‘P: R~R’ from one ring to another is a map which is compatible with the laws of composition and which carries 1 to 1, that is, a map such that ‘P(a + b) = ‘P(a) + ‘P(b), ‘P(ab) = ‘P(a)’P(b), ‘P(lR) = JR’, for all a, b E R. An isomorphism of rings is a bijective homomorphism. If there is an isomorphism R~R ” the two rings are said to be isomorphic. A word about the third part of is in order. The assumption that a homomorphism ‘P is compatible with addition implies that it is a group homomorphism R+~R’+. We know that a group homomorphism carries the identity to the identity,
so f(O) = O. But R is not a group with respect to x, and we can’t conclude that ‘P(l) = 1 from compatibility with multiplication. So the condition ‘P(l) = 1 must be listed separately. For example, the zero map R~R’ sending all elements of R to zero is compatible with + and x, but it doesn’t send 1 to 1 unless 1 = 0 in R’. The zero map isn’t a ring homomorphism unless R’ is the zero ring. The most important ring homomorphisms are those obtained by evaluating polynomials. Evaluation of real polynomials at a real number a defines a homomorphism
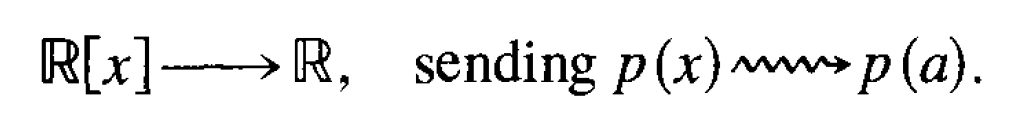

We can also evaluate real polynomials at a complex number such as i, to obtain a homomorphism