In topology, knot theory is the study of mathematical knots. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3 (in topology, a circle isn’t bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
Although people have been making use of knots since the dawn of our existence, the actual mathematical study of knots is relatively young, closer to 100 years than 1000 years. In contrast, Euclidean geometry and number theory, which have been studied over a considerable number of years, germinated because of the cultural “pull” and the strong effect that calculations and computations generated. It is still quite common to see buildings with ornate knot or braid lattice-work. However, as a starting point for a study of the mathematics of a knot, we need to excoriate this aesthetic layer and concentrate on the shape of the knot. Knot theory, in essence, is the study of the geometrical aspects of these shapes. Not only has knot theory developed and grown over the years in its own right, but also the actual mathematics of knot theory has been shown to have applications in various branches of the sciences, for example, physics, molecular biology, chemistry.
FUNDAMENTAL CONCEPTS OF KNOT THEORY
A knot, succinctly, is an entwined circle. However, throughout this book we shall think of a knot as an entwined polygon in 3-dimensional space. The reason for this is that it allows us, with recourse to combinatorial topology, 1 to exclude wild knots. Close to the point P, in a sense we may take this to be a “limit” point, the knot starts to cluster together in a concertina fashion. Therefore, in the vicinity of such a point particular care needs to be taken with the nature of the knots. We shall not in this exposition apply or work within the constraints of such (wild) knots. In fact, since wild knots axe not that common, this will be the only reference to these kind of knots. Therefore, in order to avoid the above peculiarity, we shall assume, without exception, everything that follows is considered from the standpoint of combinatorial topology. As mentioned in the preface, our intention is to avoid as ,much as possible mathematical argot and to concentrate on the substance and application of knot theory. Infrequently, as above, it will be necessary, in order to underpin an assumption, to introduce such a piece of mathematical argot. Again, as mentioned in the preface, knowledge of such concepts will not usually be required to be able to understand what follows.


Definition. On a given knot K we may perform the following four operations.
(1) We may divide an edge, AB, in space of K into two edges, AC, CB, by placing a point C on the edge AB.
(1)’ [The converse of (1)] If AC and CB are two adjacent edges of K such that if C is erased AB becomes a straight line, then we may remove the point C.
(2) Suppose C is a point in space that does not lie on K. If the triangle ABC, formed by AB and C, does not intersect K, with the exception of the edge AB, then we may remove AB and add the two edges AC and CB.
(2)’ [The converse of (2)] If there exists in space a triangle ABC that contains two adjacent edges AC and CB of K, and this triangle does not intersect K, except at the edges AC and CB, then we may delete the two edges AC, CB and add the edge AB.
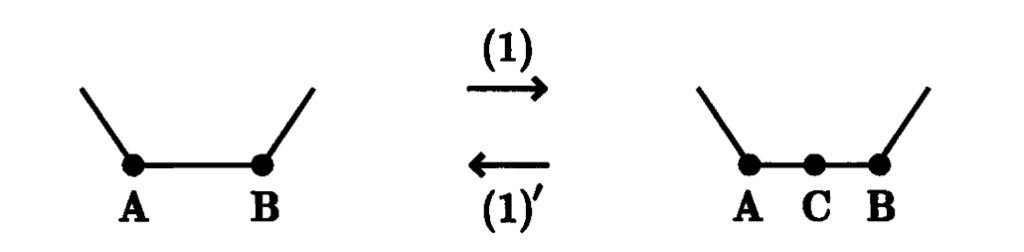

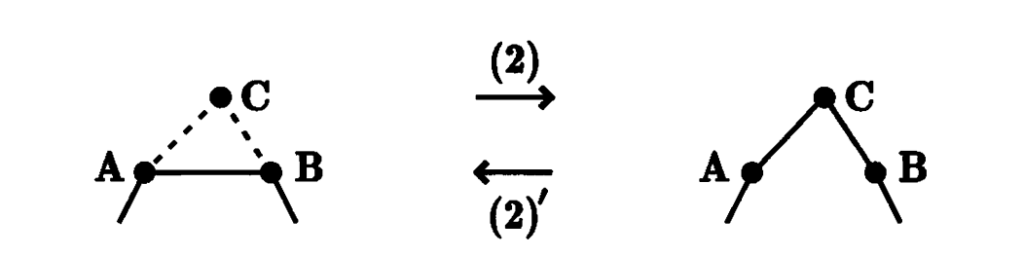

These four operations (1), (1)’, (2) and (2)’ are called the elementary knot moves.
A knot is not perceptively changed if we apply only one elementary knot move. However, if we repeat the process at different places, several times, then the resultant knot seems to be a completely different knot. For example, let us look at the two knots K1 and K2 which may be called Perko’s pair.
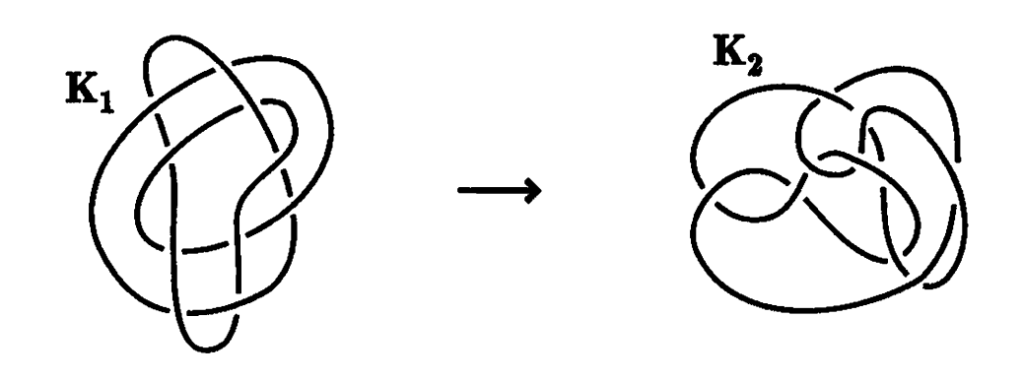

In appearance Perko’s pair of knots looks completely different. In fact, for the better part of 100 years, nobody thought otherwise. However, it is possible to change the knot K1 into the knot K2 by performing the elementary knot moves a significant number of times. This was only shown in 1970 by the American lawyer K.A. Perko. Knots that can be changed from one to the other by applying the elementary knot move are said to be equivalent or equal. Therefore, the two knots are equivalent.









Very nice work.
Excellent set of pages, 🙂 I do wish I could turn off the animation though. Having a simple mind, I get distracted 🙂
Thanks for your feedback. I’ll surely minimize the animations. STAY TUNED
I rather love the animations!