JACOBI ELLIPTIC FUNCTIONS
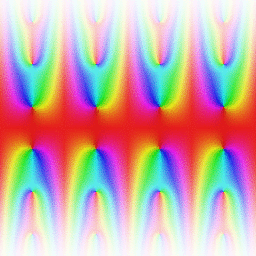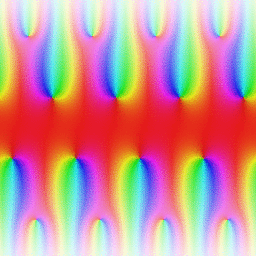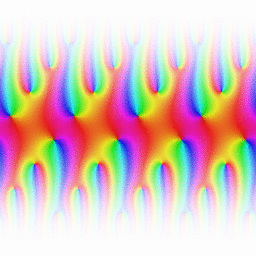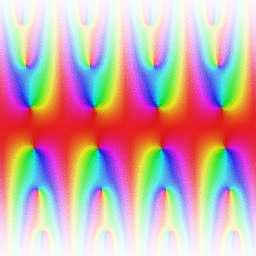

Set of basic elliptic functions, and auxiliary theta functions, that are of historical importance.


Jacobi elliptic functions are found in the description of the motion of a pendulum , as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation sn for sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi (1829).


In the mathematical field of complex analysis ELLIPTIC FUNCTIONS are a special kind of meromorphic functions, that satisfy two periodicity conditions. They are named elliptic functions because they come from elliptic integrals. Originally those integrals occurred at the calculation of the arc length of an ellipse.
Important elliptic functions are Jacobi elliptic functions and the Weierstrass p-function.

In mathematics, THETA FUNCTIONS are special functions of several complex variables. They are important in many areas, including the theories of Abelian varieties and moduli spaces, and of quadratic forms. They have also been applied to soliton theory. When generalized to a Grassmann algebra, they also appear in quantum field theory.
The most common form of theta function is that occurring in the theory of elliptic functions.
Elliptic Functions and Elliptic Curves
Definition: A complex function f(z) is called an elliptic function if it is meromorphic and doubly periodic, i.e. it admits two independent primitive periods. At least one of the two primitive periods Ω1, Ω2 of an elliptic function should be complex since the ratio Ω2/Ω1 should be nonreal. The complex plane can be tessellated by all the parallelograms formed by the period lattice obtained by translating this parallelogram over integer multiples of the two periods. The collection of the following statements are known as Liouville’s theorem.
The theory of elliptic functions provides a number of general results which we list here without proof:
- elliptic functions are fully characterized (up to a constant multiplicative factor) by their poles and zeroes, as well as their periods;
- the sum of the residues with respect to all the poles inside a single parallelogram of the period lattice is zero;
- there does not exist a non-constant elliptic function that is regular in a period parallelogram;
- the number of poles of an elliptic function in a period parallelogram counting multiplicity cannot be less than 2.
The elliptic functions are closely connected to a family of complex algebraic curves, called elliptic curves. These are curves which, in appropriate coordinates, can be cast in the form:
w2 = R(z) ,
where R is a polynomial of order p = 3 or p = 4 in z, i.e.
R(z) = αz3+ βz2 + γz + δ or R(z) = αz4 + βz3 + γz2 + δz + ǫ .
Although we can consider for real variables, it is more useful to consider this equation for complex values of w and z. The elliptic functions arise as the functions in terms of which one can naturally parametrize such curves. We can compare this to the case where the order p of the polynomial R is p ≤ 2 in which case we call the curve rational, and in which case the curve can be parametrized in terms of trigonometric functions. The simplest example of the latter is the case of the circle:
w2 + z2 = 1 ⇔ w = cos(t) , z = sin(t) .
The elliptic functions are, thus, closely related to the geometry of the above mentioned elliptic curves. Although this would be the starting point for most treatments, it is not the one adopted in this course. We will take a constructive point of view where we will start with a definition of the functions involved in terms of explicit formulae.
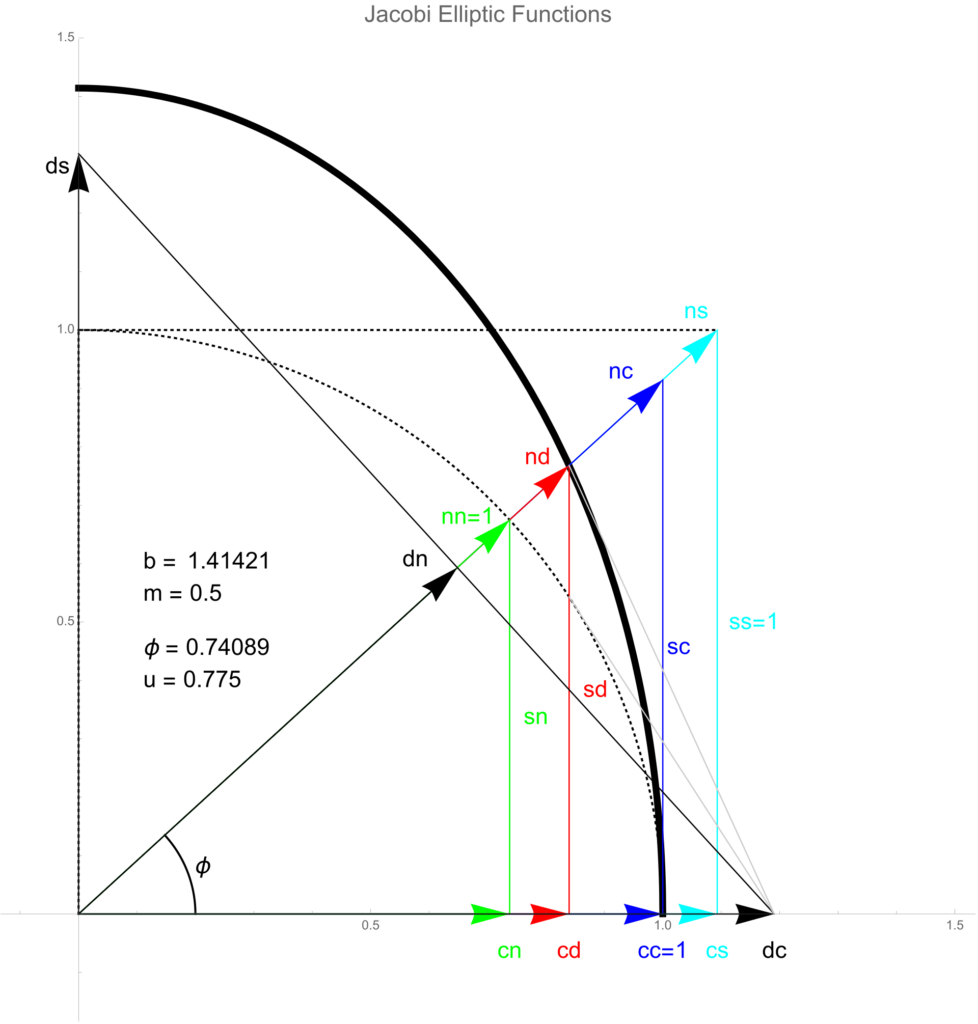

THE JACOBI ELLIPSE
The cos θ and sin θ are defined on a unit circle, with radius = 1 and angle θ = arc length of the unit circle measured from the positive x-axis. Similarly, Jacobi elliptic functions are defined on the unit ellipse, with a = 1. Let
x2 + y2 / b2 = 1, b > 1,
m = 1 – 1/b2, 0 < m < 1,
x = r cos θ and y = r sin θ then,
r ( θ ,m) = 1/√(1 – m sin2 θ).
For each angle θ the parameter
u = u ( θ ,m) = 0∫θ r ( θ ,m) dθ is computed.
On the unit circle a=b=1, u would be an arc length. While u does not carry a direct geometric interpretation in the elliptic case, it turns out to be the parameter that enters the definition of the elliptic functions. Indeed, let P=(x, y)=( r cos θ , r sin θ) be a point on the ellipse, and let P’=(x’, y’)=(cos θ, sin θ) be the point where the unit circle intersects the line between P and the origin O. Then the familiar relations from the unit circle:
x’ = r cos θ and y’ = r sin θ
read for the ellipse as:
x’ = cn (u, m) and y’ = sn (u, m).
cn (u, m) = x / r ( θ ,m) , sn (u, m) = y / r ( θ ,m) and dn (u, m) = 1 / r ( θ ,m).


DERIVATIVES d/du { pq (u, m)}
| q | |||||
| c | s | n | d | ||
| c | 0 | -ds ns | -dn sn | -m’ nd sd | |
|---|---|---|---|---|---|
| p | s | dc nc | 0 | cn dn | cd nd |
| n | dc sc | -cs ds | 0 | m cd sd | |
| d | m’ nc sc | -cs ns | -m cn sn | 0 |
To be continued…
INSPIRED BY AN ARTICLE FROM SCHOOL OF MATHEMATICS, UNIVERSITY OF LEEDS AND WIKIPEDIA. NO COPYRIGHT INFRINGEMENT INTENDED.



