CYCLIC GROUPS

A group (G, ·, e) is called cyclic if it is generated by a single element g. That is
if every element of G is equal to

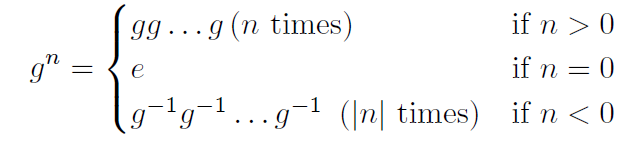
Note that if the operation is ‘+’, instead of using exponential we would use ng = g + g + g + ……

FORMALLY STATING

Definition. A group 𝐺 is a cyclic group if

In this case we say that G is a cyclic group generated by ‘a’, and obviously its an Abelian Group.

Example. The set ℤ𝑛 = {0,1, … , 𝑛 − 1}(𝑛 ≥ 1) under addition modulo 𝑛 is a cyclic group. Again, 1 and −1 (= 𝑛 − 1) are generators of ℤ𝑛. It is worthwhile to note here that while the set of integers ℤ has only two generators 1 and −1, ℤ𝑛 depending on the value of 𝑛 may have more generators apart from 1 and −1. For example,ℤ10 has 1, 3, 7, 9 (= −1) as its generators and ℤ12 has 1, 5, 7, 11 (= −1) as its generators.

Example. Consider the group 𝑈(𝑛)under multiplication modulo 𝑛, where 𝑈(𝑛) = {𝑘 ∈ ℕ ∶ 𝑘 < 𝑛 and g.c.d. (𝑘, 𝑛) = 1} .

Now for 𝑛 = 10, 𝑈(10) = {1, 3, 7, 9} = {30, 31, 33, 32} = 〈3〉. Also, 𝑈(10) = {1,3,7,9} = {70, 73, 7, 72} = 〈7〉. Thus both 3 and 7 are generators of 𝑈(10). Hence 𝑈(10) is a cyclic group. Now we will show that 𝑈(8) = {1, 3, 5, 7} is not a cyclic group. To show it we will find subgroup generated by each of the elements in 𝑈(8). Observe that

〈1〉 = {1}
〈3〉 = {1, 3} = {30, 31}
〈5〉 = {1, 5} = {50, 51}
〈7〉 = {1, 7} = {70, 71}

Therefore, 𝑈(8) ≠ 〈𝑎〉 for any 𝑎 ∈ 𝑈(8) and hence the claim. Thus we have seen that 𝑈(𝑛) is a cyclic group or not depends on the choice of 𝑛.

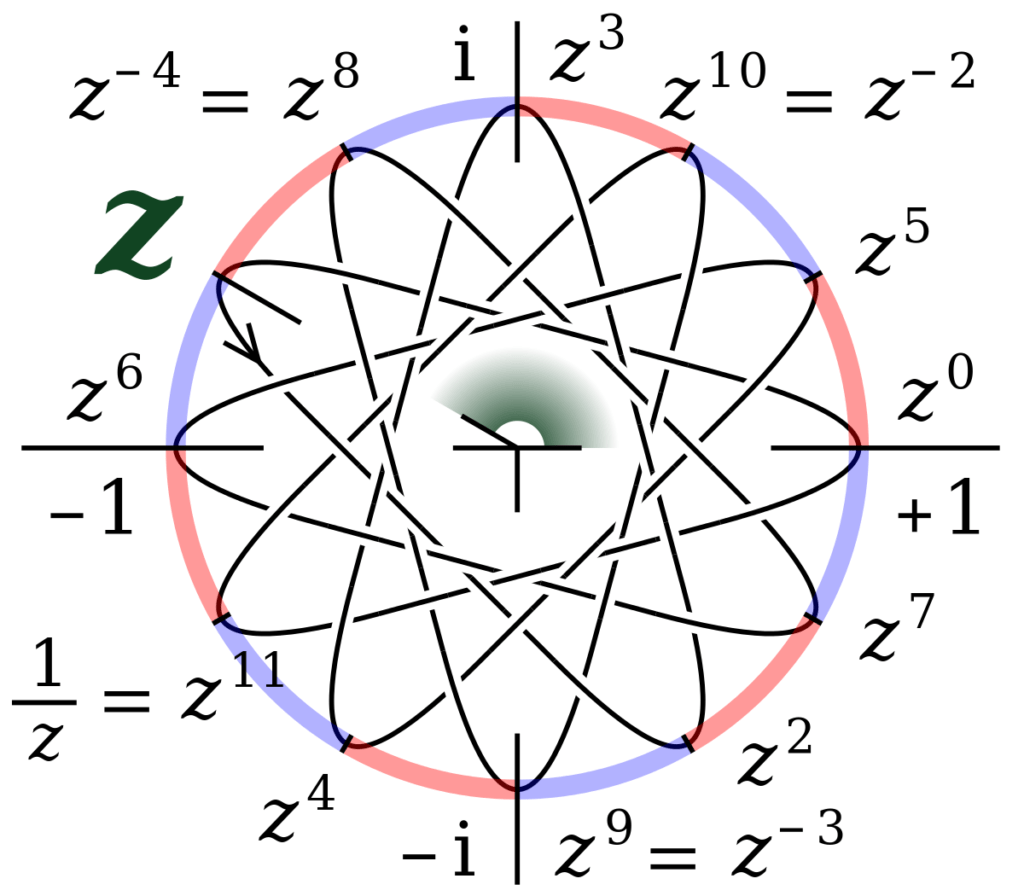
GENERATORS OF A CYCLIC GROUP

Theorem 1. For any element 𝑎 in a group 𝐺, 〈𝑎−1〉 = 〈𝑎〉 .In particular, if an element 𝑎 is a generator of a cyclic group then 𝑎−1 is also a generator of that group.

Theorem 2. For any element 𝑎 in a group 𝐺, following holds:

1. If order of 𝑎 is infinite, then all distinct powers of 𝑎 are distinct elements i.e., 𝑎𝑖 ≠ 𝑎𝑗 whenever 𝑖 ≠ 𝑗, 𝑖,𝑗 ∈ ℤ.
2. If order of 𝑎 is 𝑛 for some 𝑛 ∈ ℕ, then 〈𝑎〉 = {𝑒, 𝑎, 𝑎2, … , 𝑎𝑛−1} and 𝑎𝑖 = 𝑎𝑗 ⇔ 𝑛 divides 𝑖 − 𝑗.

Corollary. Let 𝐺 be any group and 𝑎 ∈ 𝐺 be an element of finite order 𝑛. If 𝑎^𝑘 = 𝑒 for some 𝑘 ∈ ℤ, then 𝑛 divides 𝑘.

Theorem 3. Every group of prime order is cyclic and every element other than identity is a generator of the group.

GENERATORS OF FINITE CYCLIC GROUP

Let𝐺 = 〈𝑎〉 be a finite cyclic. Then 𝐺 = 〈𝑎𝑘〉 ⇔ 𝑔.𝑐.𝑑 (𝑘, 𝑛) = 1 , where|𝐺| = 𝑛 .

Proof– Let 𝑔.𝑐.𝑑 (𝑘, 𝑛) = 1, then there exist integers 𝑠,𝑡 ∈ ℤ such that 𝑘 + 𝑛 = 1. But then 𝑎 = 𝑎1 = 𝑎𝑘+𝑛 = 𝑎𝑘𝑎𝑛 = (𝑎𝑘)𝑠(𝑎𝑛)𝑡 = (𝑎𝑘)𝑠 ∈ 〈𝑎𝑘〉. Thus 𝑎 ∈ 〈𝑎𝑘〉, which further implies that all the powers of 𝑎 belongs to 〈𝑎𝑘〉 i.e., every element of 𝐺 is in 〈𝑎𝑘〉. Hence 𝐺 = 〈𝑎𝑘〉.

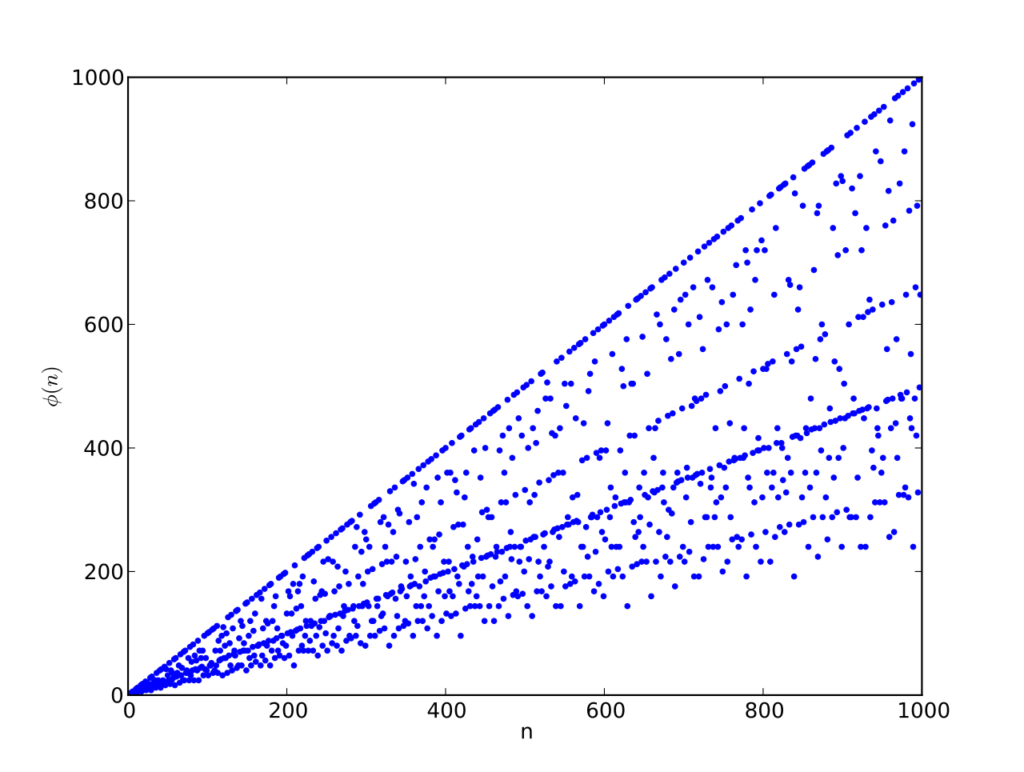
If 𝒂 is a generator of a finite cyclic group, then 𝒂𝒌 is a generator of the group if and only if 𝒌 is relatively prime to order of 𝒂. Thus a finite cyclic group of order 𝒏 has 𝝓(𝒏) generators, where 𝝓(𝒏) is the number of positive integers less than 𝒏 and relatively prime to 𝒏.

Here 𝝓(𝒏) is called Euler’s Totient Function.

In number theory, Euler’s totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as φ(n) or ϕ(n), and may also be called Euler’s phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the g.c.d.(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.

Example. The totatives of n = 9 are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since g.c.d.(9, 3) = g.c.d.(9, 6) = 3 and g.c.d.(9, 9) = 9. Therefore, φ(9) = 6. As another example, φ(1) = 1 since for n = 1 the only integer in the range from 1 to n is 1 itself, and g.c.d.(1, 1) = 1.

Euler’s product formula

It states

where the product is over the distinct prime numbers dividing n.

The proof of Euler’s product formula depends on two important facts.

The function is multiplicative

This means that if g.c.d.(m, n) = 1, then φ(mn) = φ(m) φ(n). (Outline of proof: let A, B, C be the sets of non-negative integers, which are, respectively, coprime to and less than m, n, and mn; then there is a bijection between A × B and C, by the Chinese remainder theorem.)Value for a prime power argument.

If p is prime and k ≥ 1, then

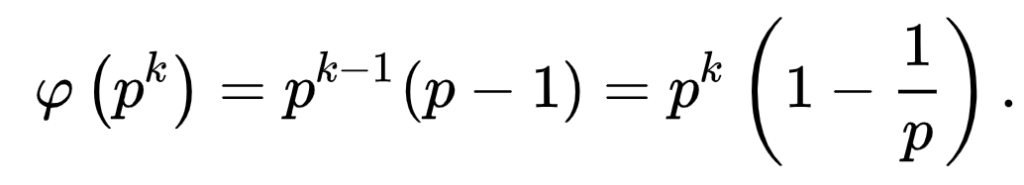
Proof: since p is a prime number the only possible values of gcd(p^k, m) are 1, p, p², …, p^k, and the only way for gcd(p^k, m) to not equal 1 is for m to be a multiple of p. The multiples of p that are less than or equal to p^k are p, 2p, 3p, …, p^{k − 1}p = p^k, and there are p^{k − 1} of them. Therefore, the other p^k − p^{k − 1} numbers are all relatively prime to p^k.

Proof of Euler’s product formula

The fundamental theorem of arithmetic states that if n > 1 there is a unique expression for n, where p₁ < p₂ < … < p_r are prime numbers and each k_i ≥ 1. (The case n = 1 corresponds to the empty product.)

Repeatedly using the multiplicative property of φ and the formula for φ(p^k) gives

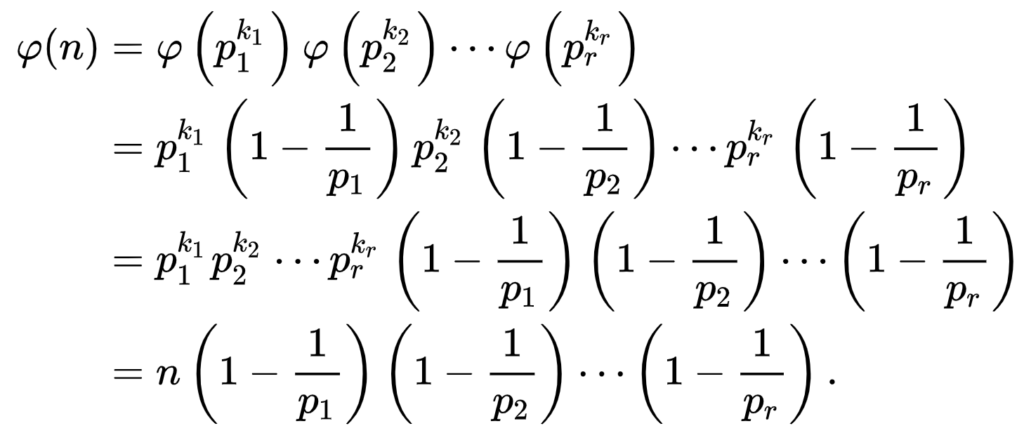
This is Euler’s product formula.

The importance of GENERATORS OF FINITE CYCLIC GROUP lies in the fact that if one of the generators of a cyclic group is known, then it gets relatively easier to find the other generators of that group. We illustrate this with the help of the example of 𝑈(50) under multiplication modulo 50.

Now, 𝑈(50) = {1,3,7,9,11,13,17,19,21,23, 27,29,31,33,37,39,41,43,47,49} and therefore |𝑈(50)| = 20. Further, from the table it is easy to see that 𝑈(50) is a cyclic group with 3 as one of its generators. Since 1, 3, 7, 9, 11, 13, 17, 19 are relatively prime to 20(=|𝑈(50)|), therefore we have 31, 33, 37, 39, 311, 313, 317, 319 that are all the generators of 𝑈(50).

𝑈(50) = 〈3〉 = 〈27〉 = 〈37〉 = 〈33〉 = 〈47〉 = 〈23〉 = 〈13〉 = 〈17〉.

Now the question to be answered is how many generators an infinite cyclic group would have and what are they.

Theorem. Order of every non-identity element in an infinite cyclic group is infinite.

GENERATORS OF INFINITE CYCLIC GROUP

Let𝐺 = 〈𝑎〉 be a cyclic group of infinite order. Then 𝐺 has precisely two generators 𝑎 and 𝑎−1.

Proof. Since 𝑎𝑎 is a generator, therefore 𝑎−1 is also a generator of 𝐺. Thus it is enough to prove that no element other than 𝑎 and 𝑎−1 is a generator of 𝐺. Let 𝑏 ∈ 𝐺 be any generator of 𝐺. Then 𝐺 = 〈𝑎〉 = 〈𝑏〉 and therefore there exist 𝑝, 𝑞 ∈ ℤ such that 𝑎 = 𝑏^𝑝and
𝑏 = 𝑎^𝑞 . Consider

𝑎 = 𝑏^𝑝 = (𝑎^𝑞 )^𝑝 = 𝑎^𝑝
⇒ 𝑎^𝑝 −1 = 𝑒
⇒ 𝑝 − 1 = 0 [Since|𝑎|infinite]
⇒ 𝑝 = 𝑞 = 1 or 𝑝 = 𝑞 = −1.
Thus either 𝑏 = 𝑎 or 𝑏 = 𝑎−1 and hence 𝑎 and 𝑎−1 are precisely the generators of 𝐺.

We can summarize the above results as follows-

Let 𝐺 be a group and let 𝑎 be any element of 𝐺. Then,

1. 〈𝑎〉 = 〈𝑎−1〉and |𝑎| = |𝑎−1| = |〈𝑎〉|.
2. |𝑎| = 𝑛 ⇔ 〈𝑎〉 = {𝑒, 𝑎, 𝑎^2, … , 𝑎^𝑛−1}
3. 𝑎^𝑘 = 𝑒 ⇔ |𝑎|divide 𝑎^𝑘
4. 𝐺 is finite cyclic group ⟹ |𝑎| divides |𝐺|
5. |𝐺| = 𝑝 (prime) and 𝑎(≠ 𝑒) ∈ 𝐺 ⟹ 𝐺 = 〈𝑎〉
6. 𝐺 = 〈𝑎〉 finite cyclic group. Then 𝐺 = 〈𝑎𝑘 〉 ⇔ 𝑔.𝑐.𝑑(𝑘, 𝑛) = 1.

Summary

Article Name

CYCLIC GROUPS

Description

In this article we will study the properties of cyclic groups and cyclic subgroups, which play a fundamental part in the classification of all Abelian groups.

Author

RAJARSHI DEY

Publisher Name

SOUL OF MATHEMATICS

Publisher Logo