The Golden Ratio

The ratio, or proportion, determined by Phi (1.618 …) was known to the Greeks as the “dividing a line in the extreme and mean ratio” and to Renaissance artists as the “Divine Proportion”  It is also called the Golden Section, Golden Ratio and the Golden Mean.

Just as pi is the ratio of the circumference of a circle to its diameter, phi is simply the ratio of the line segments that result when a line is divided in one very special and unique way.

Divide a line so that:

Definition:

Phi can be defined by taking a stick and breaking it into two portions. If the ratio between these two portions is the same as the ratio between the overall stick and the larger segment, the portions are said to be in the golden ratio. This was first described by the Greek mathematician Euclid, though he called it “the division in extreme and mean ratio,” according to mathematician George Markowsky of the University of Maine. 

You can also think of phi as a number that can be squared by adding one to that number itself, according to an explainer from mathematician Ron Knott at the University of Surrey in the U.K. So, phi can be expressed this way: phi^2 = phi + 1

This representation can be rearranged into a quadratic equation with two solutions, (1 + √5)/2 and (1 – √5)/2. The first solution yields the positive irrational number 1.6180339887… (the dots mean the numbers continue forever) and this is generally what’s known as phi. The negative solution is -0.6180339887… (notice how the numbers after the decimal point are the same) and is sometimes known as little phi.

Geometry

The number φ turns up frequently in geometry, particularly in figures with pentagonal symmetry. The length of a regular pentagon’s diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles.

There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem). However, a useful approximation results from dividing the sphere into parallel bands of equal surface area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 360°/φ ≅ 222.5°. This method was used to arrange the 1500 mirrors of the student-participatory satellite Starshine-3.

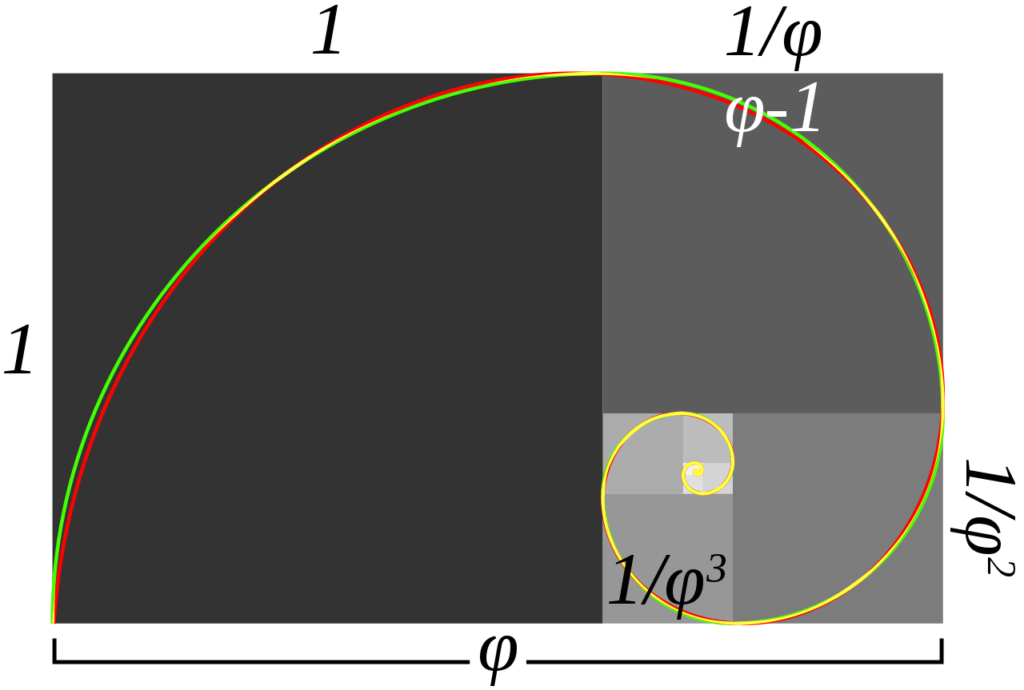
Relationship to Fibonacci sequence

The mathematics of the golden ratio and of the Fibonacci sequence are intimately interconnected. The Fibonacci sequence is:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …

A closed-form expression for the Fibonacci sequence involves the golden ratio:

The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence (or any Fibonacci-like sequence), as shown by Kepler:

In other words, if a Fibonacci number is divided by its immediate predecessor in the sequence, the quotient approximates φ; e.g., 987/610 ≈ 1.6180327868852. These approximations are alternately lower and higher than φ, and converge to φ as the Fibonacci numbers increase, and:

More generally:

where above, the ratios of consecutive terms of the Fibonacci sequence, is a case when 

Furthermore, the successive powers of φ obey the Fibonacci recurrence:

This identity allows any polynomial in φ to be reduced to a linear expression. For example:

The reduction to a linear expression can be accomplished in one step by using the relationship

where  is the kth Fibonacci number.

However, this is no special property of φ, because polynomials in any solution x to a quadratic equation can be reduced in an analogous manner, by applying:

for given coefficients a, b such that x satisfies the equation. Even more generally, any rational function (with rational coefficients) of the root of an irreducible nth-degree polynomial over the rationals can be reduced to a polynomial of degree n ‒ 1. Phrased in terms of field theory, if α is a root of an irreducible nth-degree polynomial, then , with basis 

Johannes Kepler wrote that “the image of man and woman stems from the divine proportion. In my opinion, the propagation of plants and the progenitive acts of animals are in the same ratio”. The psychologist Adolf Zeising noted that the golden ratio appeared in phyllotaxis and argued from these patterns in nature that the golden ratio was a universal law. Zeising wrote in 1854 of a universal orthogenetic law of “striving for beauty and completeness in the realms of both nature and art”.In 2010, the journal Science reported that the golden ratio is present at the atomic scale in the magnetic resonance of spins in cobalt niobate crystals. However, some have argued that many apparent manifestations of the golden ratio in nature, especially in regard to animal dimensions, are fictitious.