MODERN ALGEBRA
“The importance of mirror-reflection symmetry to our perception and aesthetic appreciation, to the mathematical theory of symmetries, to the laws of physics, and to science in general, cannot be overemphasized, and I will return to it several times. Other symmetries do exist, however, and they are equally relevant.”
― Mario Livio, The Equation That Couldn’t Be Solved: How Mathematical Genius Discovered the Language of Symmetry
Symmetry is fundamentally present since birth of Universe, and hence it has intrigued human minds and so we have analysed it. In this article we will not deal with the physical phenomenon of symmetry and reflection, instead we will delve into its mathematical impacts and how it led to the advent of a new branch of mathematics.
Let’s try to dive into the concept with an example.
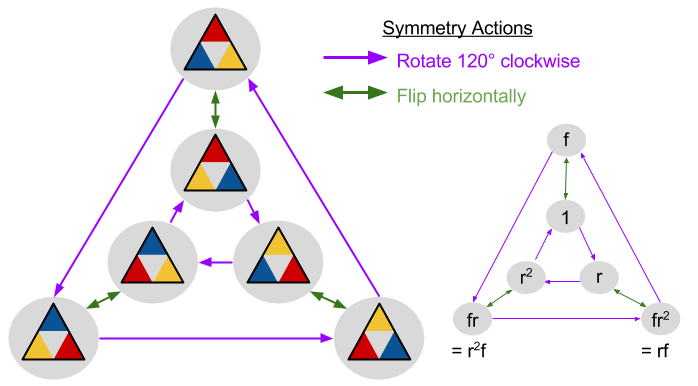

“A triangle group is
a group that can be
realized geometrically
by sequences
of reflections
across the sides of
a triangle.”
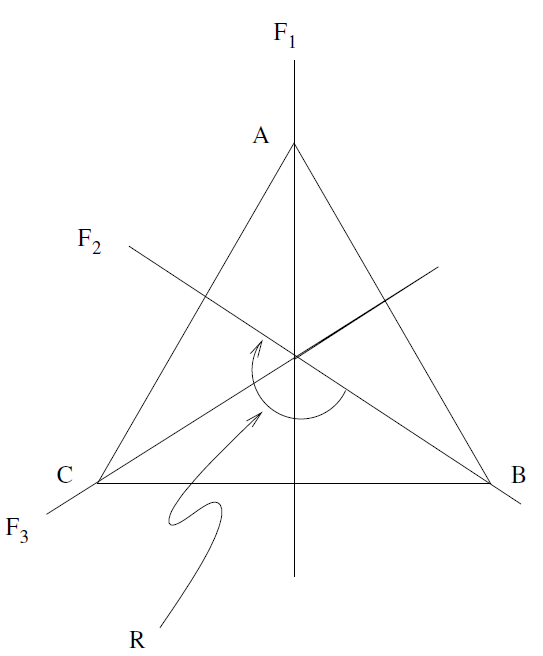

Let us take an equilateral triangle and carefully examine its symmetry group. We obviously get two sets of symmetries. First one we get by rotating the triangle by 120 degrees. Suppose that we choose clockwise as the positive direction and denote rotation through 120 degrees as R. Its quite natural to represent rotation through 240 degrees as R2 because it has been applied twice. Hence, by applying R thrice, represented by R3 we would get back where we started. Note that the symmetry rotation through 120 degrees anticlockwise, could be represented as R-1. This is the same as rotation through 240 degrees clockwise, so that R-1 = R2. The other sets of symmetries are flips. For example, one can draw a vertical line through the top corner and flip about this line. Call this operation F = F1. Note that F2 = I, representing the fact that flipping twice does nothing.
The set of symmetries we have created so far is then equal to {I, R, R2, F1, F2, F3}.