RIEMANN HYPOTHESIS
The German mathematician G.F.B. Riemann (1826 – 1866) observed that the frequency of prime numbers is very closely related to the behavior of an elaborate function
ζ(s) = 1 + 1/2s + 1/3s + 1/4s + …
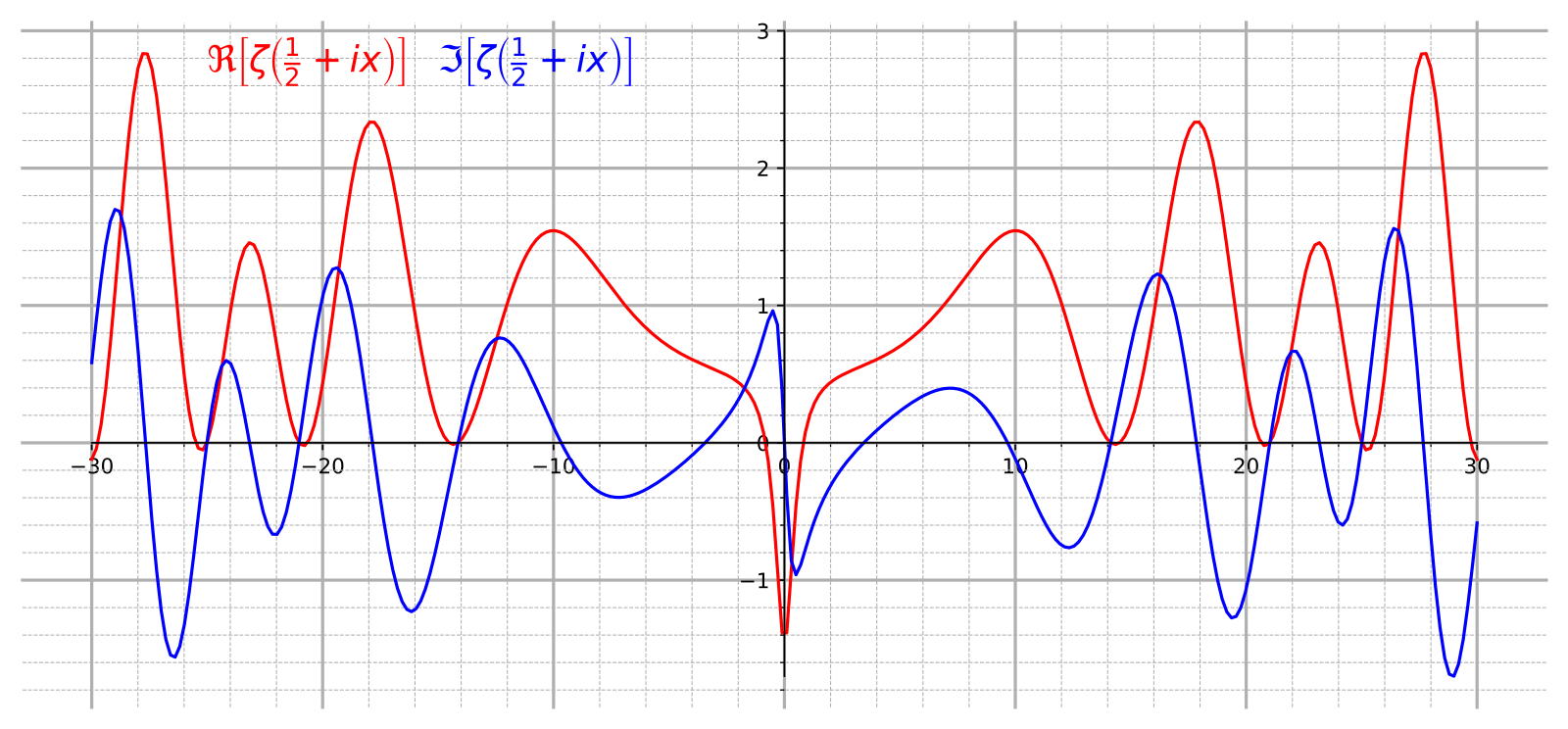
called the Riemann Zeta function. The Riemann hypothesis asserts that all interesting solutions of the equation ζ(s) = 0 lie on a certain vertical straight line.
This has been checked for the first 10,000,000,000,000 solutions. A proof that it is true for every interesting solution would shed light on many of the mysteries surrounding the distribution of prime numbers.
Yet, This problem is: Unsolved
The Problem
The Riemann zeta function is the function of the complex variable s, defined in the half-plane1 R(s) > 1 by the absolutely convergent series
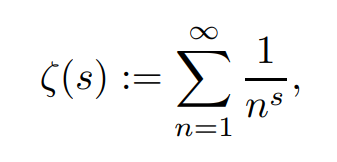
and in the whole complex plane C by analytic continuation. As shown by Riemann, ζ(s) extends to C as a meromorphic function with only a simple pole at s =1, with residue 1, and satisfies the functional equation
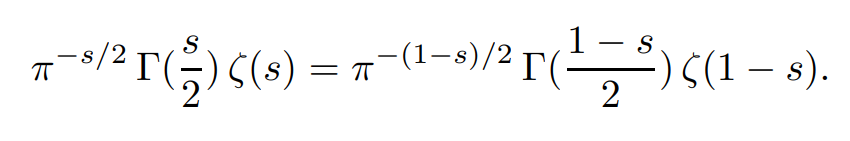
In 1859, Riemann obtained an analytic formula for the number of primes up to a preassigned limit. This formula is expressed in terms of the zeros of the zeta function, namely the solutions ρ ∈ C of the equation ζ(ρ) = 0.
In this paper, Riemann introduces the function of the complex variable t defined by,
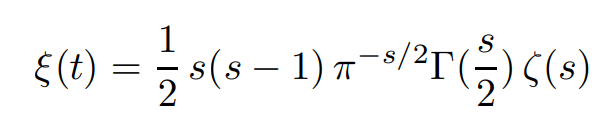
with s = 1/2 +it, and shows that ξ(t) is an even entire function of t whose zeros have imaginary part between −i/2 and i/2.
Riemann hypothesis. The nontrivial zeros of ζ(s) have real part equal to 1/2 .
Evidence for the Riemann hypothesis.
Interestingly enough, the first numerical computation of the first few zeros of the zeta function already appears in Riemann’s Nachlass. A rigorous verification of the Riemann hypothesis in a given range can be done numerically as follows. The number N(T ) of zeros of ζ(s) in the rectangle R with vertices at −1 − iT, 2 −iT, 2 + iT, −1 + iT is given by Cauchy’s integral
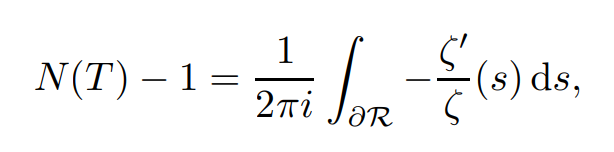
provided T is not the imaginary part of a zero (the −1 in the left-hand side of
this formula is due to the simple pole of ζ(s) at s =1 ). The zeta function and
its derivative can be computed to arbitrary high precision using the MacLaurin summation formula or the Riemann-Siegel formula [Sie]; the quantity N(T ) − 1, which is an integer, is then computed exactly by dividing by 2πi the numerical evaluation of the integral, and rounding off its real part to the nearest integer (this is only of theoretical interest and much better methods are available in practice for computing N(T ) exactly). On the other hand, since ξ(t) is continuous and real for real t, there will be a zero of odd order between any two points at which ξ(t) changes sign. By judiciously choosing sample points, one can detect sign changes of ξ(t) in the interval [−T,T ]. If the number of sign changes equals N(T ), one concludes that all zeros of ζ(s) in R are simple and satisfy the Riemann hypothesis. In this way, it has been shown by van de Lune, te Riele and Winter [LRW] that the first 1.5 billion zeros of ζ(s), arranged by increasing positive imaginary part, are simple and satisfy the Riemann hypothesis.
Lindelöf hypothesis and growth of the Zeta Function
The Riemann hypothesis has various weaker consequences as well; one is the Lindelöf hypothesis on the rate of growth of the zeta function on the critical line, which says that, for any ε > 0,
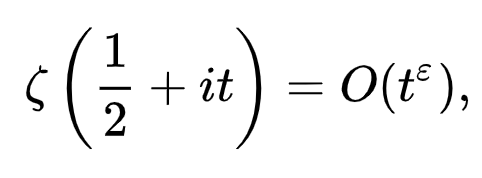
as 
. The Riemann hypothesis also implies quite sharp bounds for the growth rate of the zeta function in other regions of the critical strip. For example, it implies that
so the growth rate of ζ(1+it) and its inverse would be known up to a factor of 2.
The Riemann hypothesis was one of the famous Hilbert problems — number eight of twenty-three. It is also one of the seven Clay Millennium Prize Problems.
For further discussion on this subject please subscribe.
