We think mathematics to be a subject too coarse to have a connection to any spirit, let alone to have its own. But Mathematicians are probably the only people to have named a theorem ‘THE SOUL THEOREM’. The soul theorem is a theorem of Riemannian geometry that largely reduces the study of complete manifolds of non-negative sectional curvature to that of the compact case. Every compact manifold is its own soul. In 1972, Cheeger and Gromoll proved the theorem by the generalization of a 1969 result of Gromoll and Wolfgang Meyer. The related soul conjecture was formulated by Gromoll and Cheeger in 1972 and proved by Grigori Perelman in 1994 with an astonishingly concise proof.
The theorem states,
If (M, g) is a complete connected Riemannian manifold with sectional curvature K ≥ 0, then there exists a compact totally convex, totally geodesic submanifold S whose normal bundle is diffeomorphic to M. (Note that the sectional curvature must be non-negative everywhere, but it does not have to be constant.) Such a submanifold S is called a soul of (M, g).
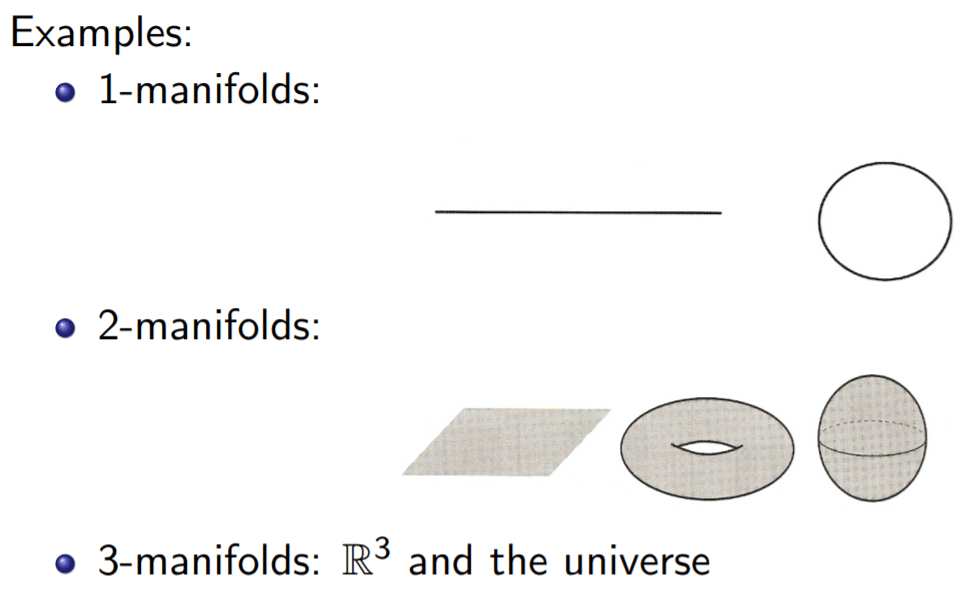
Manifolds in mathematics are topological spaces that resembles Euclidean spaces near each point locally. An n-dimensional manifold is precisely a topological space with the property that each point has a neighborhood that is homeomorphic to the Euclidean space of dimension n. In topology, two objects have the same shape if one can be deformed into the other without cutting or gluing. Objects with the same shape are called homeomorphic.

SOUL CONJECTURE
The Cheeger and Gromoll’s soul conjecture states,
Suppose (M, g) is complete, connected and non-compact with sectional curvature K ≥ 0, and there exists a point in M where the sectional curvature (in all sectional directions) is strictly positive. Then the soul of M is a point; equivalently M is diffeomorphic to Rn.
Grigori Perelman established that in the general case K ≥ 0, Sharafutdinov’s retraction P : M → S is a submersion and hence proved the soul conjecture.
In this note we consider complete noncompact Riemannian manifolds M of nonnegative sectional curvature. The structure of such manifolds was discovered by Cheeger and Gromoll : M contains a (not necessarily unique) totally convex and totally geodesic submanifold S without boundary, 0 < dimS < dimM, such that M is diffeomorphic to the total space of the normal bundle of S in M . (S is called a soul of M.) In particular, if S is a single point, then M is diffeomorphic to a Euclidean space. This is the case if all sectional curvatures of M are positive, according to an earlier result of Gromoll and Meyer. Cheeger and Gromoll conjectured that the same conclusion can be obtained under the weaker assumption that M contains a point where all sectional curvatures are positive. A contrapositive version of this conjecture expresses certain rigidity of manifolds with souls of positive dimension. It was verified in the cases dim S = 1 and codimS = 1, and by Marenich, Walschap, and Strake in the case codimS = 2.
EXAMPLE,
As a very simple example, take M to be Euclidean space Rn. The sectional curvature is 0 everywhere, and any point of M can serve as a soul of M. Now take the paraboloid M = {(x, y, z) : z = x2 + y2}, with the metric g being the ordinary Euclidean distance coming from the embedding of the paraboloid in Euclidean space R3. Here the sectional curvature is positive everywhere, though not constant. The origin (0, 0, 0) is a soul of M. Not every point x of M is a soul of M, since there may be geodesic loops based at x, in which case 
Citation
Perelman, G. Proof of the soul conjecture of Cheeger and Gromoll. J. Differential Geom. 40 (1994), no. 1, 209–212. doi:10.4310/jdg/1214455292.