Ricci Flow

“As far as the laws of mathematics refer to reality, they are not certain;
and as far as they are certain, they do not refer to reality.“

-Albert Einstein

In 1900, Henri Poincare put for a conjecture that colloquially states that
“If it walks like a sphere and it quacks like a sphere, it is a sphere.” This statement, known as the Poincare conjecture, became one of the early questions in a field now called “low-dimensional topology” and proved itself to be extremely subtle and intractable. It attracted the attention of many great mathematicians and attempts to solve it lead to the development of powerful tools.

Introduction

Ricci flow, introduced by Richard S. Hamilton in 1982, is a fundamental concept in differential geometry and geometric analysis. It involves deforming the metric of a Riemannian manifold in a way that smooths out irregularities in its shape, much like how heat diffuses through a material. This concept has not only deepened our understanding of geometric structures but also played a crucial role in the proof of the Poincaré Conjecture by Grigori Perelman. This article explores the mathematical foundations of Ricci flow, provides detailed insights into its behavior, and discusses its significant applications in various fields of mathematics and theoretical physics.

Mathematical Foundation

Riemannian Manifolds–

A Riemannian manifold \(M\) is a smooth manifold equipped with a Riemannian metric \(g\), which is a smoothly varying positive-definite inner product on the tangent space at each point. The metric \(g\) allows for the definition of geometric quantities such as lengths of curves, angles between vectors, and volumes of regions.

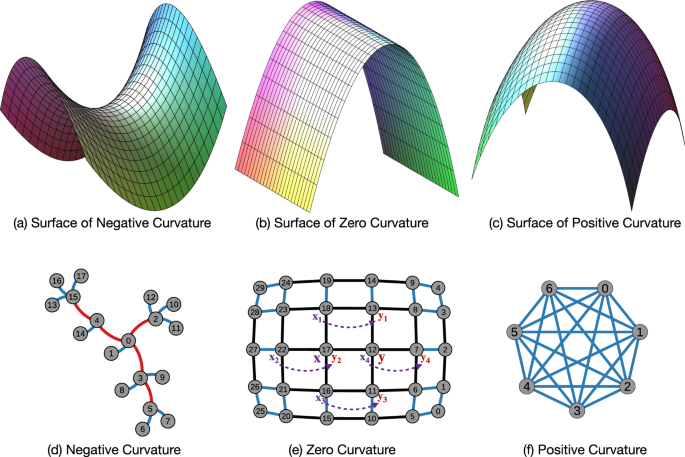
Ricci Curvature–

The Ricci curvature tensor \(\text{Ric}(g)\) is derived from the Riemann curvature tensor \(R\) by taking a trace over two of its indices:

\[\text{Ric}_{ij} = R_{ikj}^k.\]

Here, \(R_{ikj}^k\) represents the components of the Riemann curvature tensor. Ricci curvature encapsulates the extent to which the volume of a small geodesic ball in the manifold deviates from that in Euclidean space. Specifically, it measures the average sectional curvature along various directions.

The Ricci Flow Equation–

The Ricci flow equation describes how the Riemannian metric \(g\) evolves over time \(t\):

\[\frac{\partial g_{ij}}{\partial t} = -2\text{Ric}_{ij}(g(t)).\]

This equation indicates that the metric is adjusted at each point in the direction opposite to its Ricci curvature. High curvature regions shrink, while low curvature regions expand, leading to a more uniform geometry over time.

Properties and Behavior of Ricci Flow

Short-Time Existence and Uniqueness–

Hamilton’s foundational result guarantees the short-time existence and uniqueness of the Ricci flow. For a given smooth initial metric \(g(0)\) on a compact manifold \(M\), there exists a unique smooth solution \(g(t)\) to the Ricci flow equation for a short duration. This ensures that the flow can be initiated from any smooth starting point.

Long-Time Behavior and Singularities–

As Ricci flow progresses, singularities can form where the curvature becomes unbounded. Understanding and resolving these singularities is crucial for comprehending the long-term behavior of the flow. Techniques such as blow-up analysis, which involves rescaling the metric near singularities, and the introduction of surgeries to modify the manifold at singular points, are employed to study these phenomena.

Hamilton’s Program and Perelman’s Contributions

Hamilton’s program aimed to use Ricci flow to prove the Thurston Geometrization Conjecture, which classifies all compact 3-manifolds based on their geometric structures. Grigori Perelman’s work in the early 2000s introduced several innovative ideas, including entropy functionals and \(\kappa\)-solutions, to handle singularities and understand the flow’s behavior at large times.

Perelman’s Entropy Functionals–

Perelman introduced the notion of the \(\mathcal{F}\)-functional and the \(\mathcal{W}\)-entropy:

\[\mathcal{F}(g,f)=\int_{M}​(R+∣\nabla f∣^2)e^{−f}d\mu\]

\[\mathcal{W}(g,f,\tau) = \int_{M}[\tau​(R+∣\nabla f∣^2)+f-n](4\pi\tau)^{-\frac{n}{2}}e^{−f}d\mu.\]

These functionals are designed to be monotonic under the Ricci flow, providing powerful tools for analyzing the flow’s behavior and proving the non-collapsing results needed to control the formation of singularities.

Ricci Flow with Surgery–

To continue the flow past singularities, Perelman refined Hamilton’s technique of Ricci flow with surgery. This involves cutting out singular regions and gluing in standard geometric pieces to maintain smoothness. By carefully controlling the surgeries, Perelman was able to extend the flow indefinitely and classify the possible long-term behaviors of 3-manifolds.

Applications of Ricci Flow

Topology and Geometry of 3-Manifolds–

The most celebrated application of Ricci flow is in the proof of the Poincaré Conjecture and the Thurston Geometrization Conjecture. Perelman’s work demonstrated that Ricci flow could be used to decompose 3-manifolds into pieces with uniform geometric structures, thus achieving a complete classification of these spaces.

Geometric Analysis–

Ricci flow has become a central tool in geometric analysis, providing insights into the structure and behavior of Riemannian manifolds. It has been used to prove various results about the existence and uniqueness of geometric structures, as well as to study the stability and rigidity of these structures under deformation.

Theoretical Physics–

In theoretical physics, Ricci flow has applications in the study of the renormalization group flow in quantum field theory and string theory. The evolution of the metric under Ricci flow resembles the behavior of physical systems under renormalization, providing a deep connection between geometry and physics.

Detailed Mathematical Insights

Heat Equation Analogy–

Ricci flow is often compared to the heat equation due to their similar smoothing effects. The heat equation for a scalar function \(u\) is given by:

\[\frac{\partial u}{\partial t} = \Delta u\]

where \(\Delta\) is the Laplacian operator. The heat equation causes uuu to become more uniform over time, analogous to how Ricci flow smooths out the metric.

Maximum Principle–

A crucial tool in the analysis of Ricci flow is the maximum principle, which provides bounds on the behavior of the flow. For instance, Hamilton used the maximum principle to derive curvature estimates, showing that certain curvature conditions are preserved under the flow.

Ricci Solitons–

Ricci solitons are self-similar solutions to the Ricci flow equation of the form:

\[\text{Ric}(g) + \nabla^2 f = \lambda g\]

where \(f\) is a smooth function on the manifold and \(\lambda\) is a constant. Ricci solitons model the formation of singularities and play a key role in the classification of singularity models.

Conclusion

Ricci flow is a powerful and versatile tool in mathematics, with profound implications in geometry, topology, and theoretical physics. Its ability to smooth out the geometry of manifolds and handle singularities has led to significant breakthroughs, most notably in the proof of the Poincaré Conjecture. As research in this area continues, Ricci flow promises to yield further insights and applications, cementing its place as a cornerstone of modern mathematical theory. The detailed mathematical insights provided by tools like the maximum principle, Ricci solitons, and entropy functionals continue to drive advancements in understanding the deep connections between geometry and topology.