Fascinating Quaternions

Let us imagine taking strolls in One Dimension. Well we seem to only move forward and backward along a single line in a fixed direction. We can imagine walking along the real number line. Now if we represent our position in this situation we would be using One Dimensional numbers.

Now lets move onto a Two Dimensional walk. We can simply represent these as moving around in a flat plane with definite X and Y axes to pin point our position. The question arises, ‘Can we denote our position by a single number?’ The answer is fascinating in itself because with this we delve into probably the most interesting space of numbers. The position in 2-D is represented by complex numbers. Its a very simple concept to denote a number using two directions to reach it from any other number.

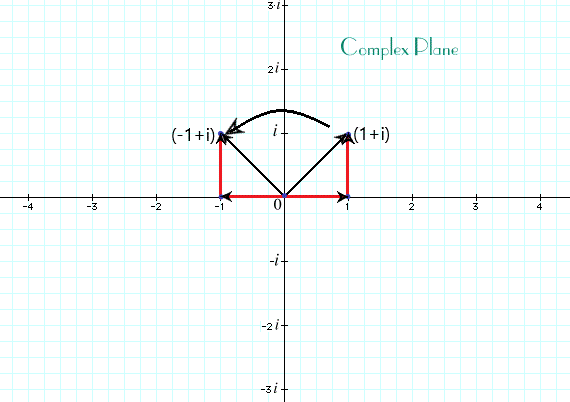
Travelling in a complex plane is very simple. We have to select an initial position first. Lets talk about this example and select the initial position as the origin. Then moving a unit in positive x-direction, pausing for a while and then taking a counter-clockwise turn of 90 degrees and moving another unit but now in positive y-direction. We have reached (1+i). Its just like another number, we can add two of them together and multiply also. For example lets add up (1+i) and (-1+i) we get 2i on the positive y-axis. Again lets multiply i and (1+i). Now here is a little catch. What is ‘i’ we are talking so much about? Its called ‘iota’ which represents the square root of negative 1 [(-1)^(1/2)]. So if we multiply ‘i’ to itself we get back negative one. Lets check for ourselves, multiplying i and 1+i, we get i*(1+i)=i*1+i*i=i-1=-1+i. We turn 90 degrees counter-clockwise from (1+i) ending up in (-1+i). Hence we see that rotation is feasible.

Now the real deal, to represent a single number for three dimensions.

By now many of you are thinking that if we can represent a 2-D number by ‘a+ib’ form then quite intuitively a 3-D number can be represented by something of the form ‘a+ib+jc’. Well it is a 3-D number but we cannot use it to move about in 3-D space. But here is where we get to see a brilliant mathematical mind excel.

The advent of Quaternions.

One fine day Sir William Rowan Hamilton was taking strolls by a canal with his wife and the same question was hovering in his mind “How to represent a position in 3-D using 3-D number?” Then he was struck by an idea and he ran to a bridge over the canal and engraved his findings which now has been developed into an embedded stone carving.

The mind blowing idea was to use four dimensions to define a position and to move about in 3-D. Hence, the formula Sir Hamilton came up with was quite similar to the concept of complex numbers is as stated below- i^2=j^2=k^2=i*j*k=-1. Simple yet brilliant. This theorem gained massive popularity as it opens up a vast field to work with. Now that we know that these are actually 4-D so the number can be written as ‘a+ib+cj+dk’. We can now freely rotate and move about in 3-D. Suppose we take a point P(xi+yj+zk) in a 3-D plane. We need h=a+bi+cj+dk and h*=a-bi-cj-dk. The changed coordinates will be P*= h x P x h*.

Like the Quaternions there are Octonions but as we go up these lose some properties and become quite faint and is not studied widely.