Sylow theorems are a collection of theorems named after the Norwegian mathematician Peter Ludwig Sylow (1872) that give detailed information about the number of subgroups of fixed order that a given finite group contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups.
Sylow’s theorems and their proofs.
Definitions. Let G be a group, and let p be a prime number.
• A group of order pk for some k ≥ 1 is called a p-group. A subgroup of order pk for some k ≥ 1 is called a p-subgroup.
• If |G| = pα m where p does not divide m, then a subgroup of order pα is called a Sylow p-subgroup of G.
Notation. Sylp(G) = the set of Sylow p-subgroups of G
np(G) = the # of Sylow p-subgroups of G = |Sylp(G)|
Diving Into Details
Let G be a group of order pα m, where p is a prime, m ≥ 1, and p does not divide m. Then:
- Sylp(G) not equal to ∅, i.e. Sylow p-subgroups exist.
- All Sylow p-subgroups are conjugate in G, i.e., if P1 and P2 are both Sylow p-subgroups, then there is some g ∈ G such that P1 = g P1g −1. In particular, np(G) = (G : NG(P)).
- Any p-subgroup of G is contained in a Sylow p-subgroup.
- np(G) ≡ 1 mod p.
First Sylow Theorem: There is a subgroup of G whose order is pe.
Proof: We let g be the set of all subsets of G of order pe. One of these subsets is the subgroup we are looking for, but instead of finding it directly we will show that one of these subsets has a stabilizer of order pe. The stabilizer will be the required subgroup.
Lemma. The number of subsets of order pe in a set of n = pem elements
(p not dividing m) is the binomial coefficient
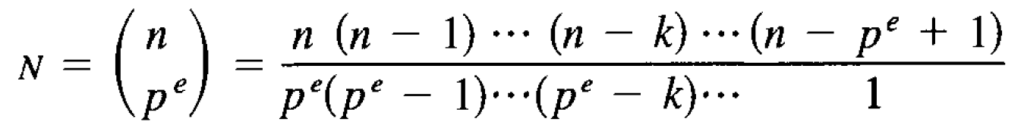

Moreover N is not divisible by p.
Proof. It is a standard fact that the number of subsets of order pe: is this binomial coefficient. To see that N is not divisible by p, note that every time p divides a term (n – k) in the numerator of N, it also divides the term (pe – k) of the denominator exactly the same number of times: If we write k in the form k = pi l, where p does not divide l, then i < e. Therefore (n – k) and (pe – k) are both divisible by pi but not divisible by p1+i.
We decompose g into orbits for the operation of left multiplication, obtaining the formula.
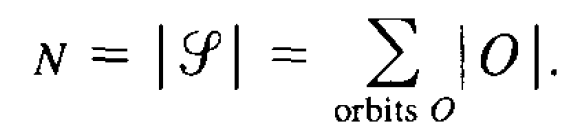

Since p does not divide N, some orbit has an order which is not divisible by p, say the orbit of the subset U.
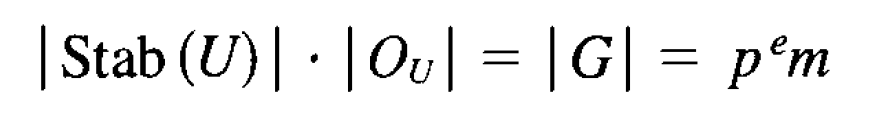

Second Sylow Theorem: Let K be a subgroup of G whose order is divisible by p, and let H be a Sylow p-subgroup of G. There is a conjugate subgroup H’ = gHg– 1 such that K n H’ is a Sylow subgroup of K.
Proof: We are given a subgroup K and a Sylow subgroup H of G, and we are to show that for some conjugate subgroup H I of H, the intersection K n H I is a Sylow subgroup of K. Let S denote the set of left cosets G/H. The facts that we need about this set are that G operates transitively, that is, the set forms a single orbit, and that H is the stabilizer of one of its elements, namely of s = 1H. So the stabilizer of as is the conjugate subgroup aHa-1. We restrict the operation of G to K and decompose S into K-orbits. Since H is a Sylow subgroup, the order of S is prime to p. So there is some K-orbit O whose order is prime to p. Say that O is the K-orbit of the element as. Let H’ denote the stabilizer aHa-1 of as for the operation of G. Then the stabilizer of as for the restricted operation of K is obviously H’ n K, and the index [K:H’nK] is |O|, which is prime to p. Also, since it is a conjugate of H, H’ is ap-group. Therefore H’ n K is a p -group. It follows that H’ n K is a Sylow subgroup of K.
Third Sylow Theorem: Let |G| = n, and n = pem. Let s be the number of Sylow p-subgroups. Then s divides m and is congruent 1 (modulo p): s|m, and s = ap + 1 for some integer a ≥ O.
Proof: The Sylow subgroups of G are all conjugate to a given one, say to H. So the number of Sylow subgroups is s = [G:N], where N is the normalizer of H. Since H⊂N, [G:N] divides [G:H] = m. To show s ≡ 1 (modulo p), we decompose the set {H1, … , Hs} of Sylow subgroups into orbits for the operation of conjugation by H = H1. An orbit consists of a single group Hi if and only if H is contained in the normalizer M of Hi. If so, then H and Hi are both Sylow subgroups of M, and Hi is normal in M. There is only one H orbit of order 1, namely {H}. The other orbits have orders divisible by p because their orders divide |H|, by the Counting Formula. This shows that s ≡ 1 (modulo p).