As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each mutual forces, and have marched together towards perfection.
Joseph-Louis Lagrange
Partial differential equations can be formed by the elimination of arbitrary constants or arbitrary functions. If we have f (x, y) then we have the following representation of partial derivatives,
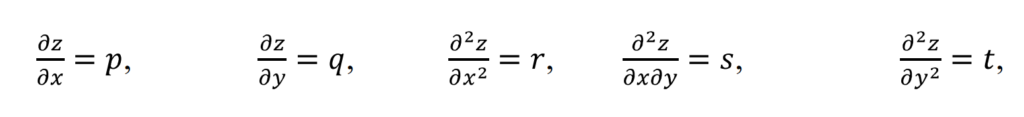

Let F (x,y,z,p,q) = 0 be the first order differential equation. It contains three types of variables, where x and y are independent variables and z is dependent variable.
A short classification of partial differential equations (PDE) –
Linear equation. A first order equation f (x, y, z, p, q) = 0 is known as linear if it is linear in p, q and z, that is, if given equation is of the form P(x, y) p + Q(x, y) q = R(x, y) z + S(x, y).
For example, yx2p + xy2q = xyz + x2y3 and p + q = z + xy are both first order linear partial differential equations.
Semi-linear equation. A first order partial differential equation f (x, y, z, p, q) = 0 is known as a semi-linear equation, if it is linear in p and q and the coefficients of p and q are functions of x and y only i.e. if the given equation is of the form P(x, y) p + Q(x, y) q = R(x, y, z)
For example, xyp + x2yq = x2y2z2 and yp + xq = (x2z2/y2) are both first order semi-linear partial differential equations.
Quasi-linear equation. A first order partial differential equation f(x, y, z, p, q) = 0 is known as quasi-linear equation, if it is linear in p and q, i.e., if the given equation is of the form P(x, y, z) p + Q(x, y, z) q = R(x, y, z)
For example, x2zp + y2zp = xy and (x2 – yz) p + (y2 – zx) q = z2 – xy are first order quasi-linear partial differential equations.
Non-linear equation. A first order partial differential equation f(x, y, z, p, q) = 0 which does not come under the above three types, in known as a non-liner equation.
For example, p2 + q2 = 1, p q = z and x2 p2 + y2 q2 = z2 are all non-linear partial differential equations.
THE EQUATION
A particular Quasi-linear partial differential equation of order one is of the form Pp + Qq = R, where P, Q and R are functions of x, y, z. Such a partial differential equation is known as Lagrange equation.
For Example xyp + yzq = zx is a Lagrange equation.
Theorem. The general solution of Lagrange equation Pp + Qq = R, is
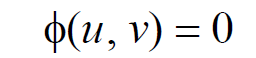

where Ф is an arbitrary function and u(x, y, z) = c1 and v(x, y, z) = c2 are two independent solutions of (dx)/P = (dy)/Q = (dz)/R. Here, c1 and c2 are arbitrary constants and at least one of u, v must contain z.
Proof. Lets number the equations for simplification.
- Pp + Qq = R
- Ф(u, v) = 0
- u(x, y, z) = c1 and v(x, y, z) = c2
- (dx)/P = (dy)/Q = (dz)/R
Differentiating (2) partially w.r.t. ‘x’ and ‘y’, we get equations 5 and 6,
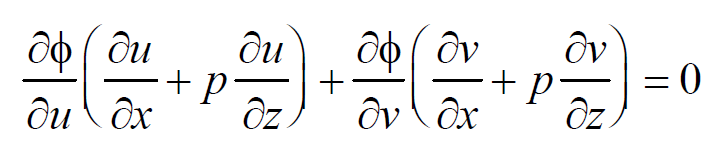

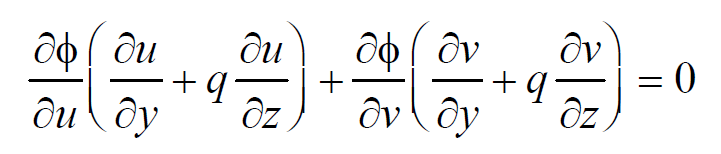

Eliminating ∂Ф / ∂u and ∂Ф/ ∂v between (5) and (6), we have,
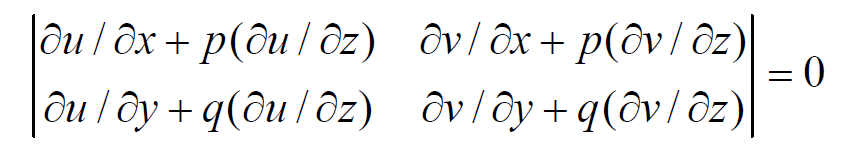

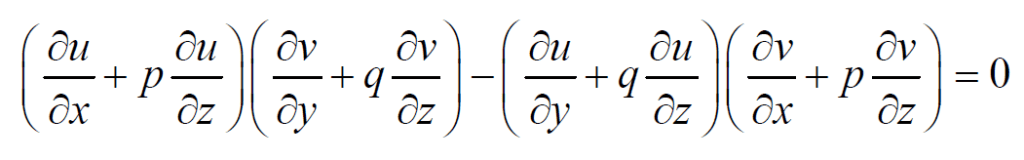

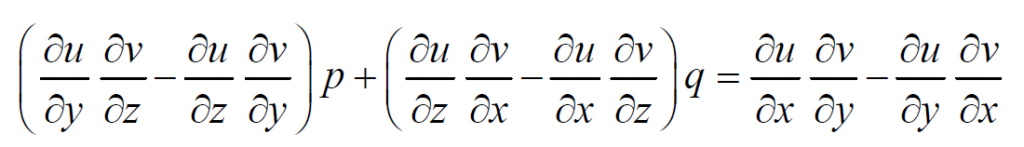

Hence, (2) is a solution of this equation.
Taking the differentials of u(x, y, z) = c1 and v(x, y, z) = c2, we get,
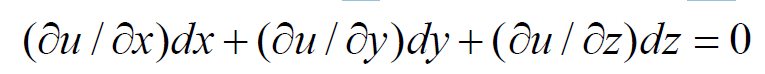

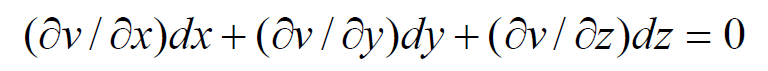

As u and v are independent functions, the ratios dx : dy : dz, gives
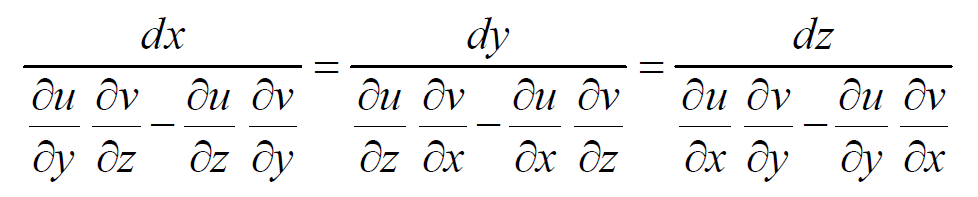

Comparing equations we obtain,
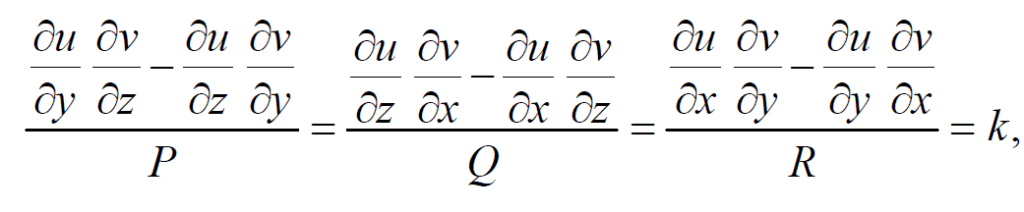

We can imply that,
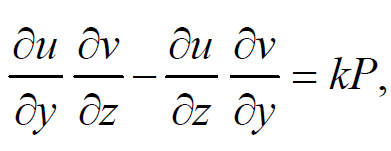

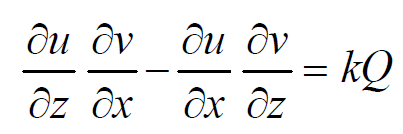

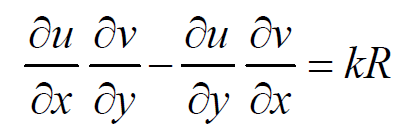

Substituting these values we get, k(Pp + Qq) = kR or Pp + Qq = R, which is the given equation (1). Therefore, if u(x, y, z) = c1 and v(x, y, z) = c2 are two independent solutions of the system of differential equations (dx)/P = (dy)/Q = (dz)/R, then Ф(u, v) = 0 is a solution of Pp + Qq = R, Ф being an arbitrary function.
Equations (4) are called Lagrange’s auxillary (or subsidiary) equations for (1).

Steps for solving Pp + Qq = R by Lagrange’s method.
Step 1. Put the given linear partial differential equation of the first order in the standard form
Pp + Qq = R. …(1)
Step 2. Write down Lagrange’s auxiliary equations for (1) namely,
(dx)/P = (dy)/Q = (dz)/R …(2)
Step 3. Solve equation (2). Let u(x, y, z) = c1 and v(x, y, z) = c2 be two independent solutions of (2).
Step 4. The general solution (or integral) of (1) is then written in one of the following three equivalent forms :
Ф(u, v) = 0, u = Ф(v) or v = Ф(u), Ф being an arbitrary function.
FOR TUTORIAL SHEETS AND REFINED MATERIALS SUBSCRIBE TO RECEIVE THEM VIA EMAIL.